eJournal: uffmm.org
ISSN 2567-6458, 19.Juni 2022 – 30.December 2022
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de
CONTEXT
This text is part of the Philosophy of Science theme within the the uffmm.org blog.
This is work in progress:
- The whole text shows a dynamic, which induces many changes. Difficult to plan ‘in advance’.
- Perhaps, some time, it will look like a ‘book’, at least ‘for a moment’.
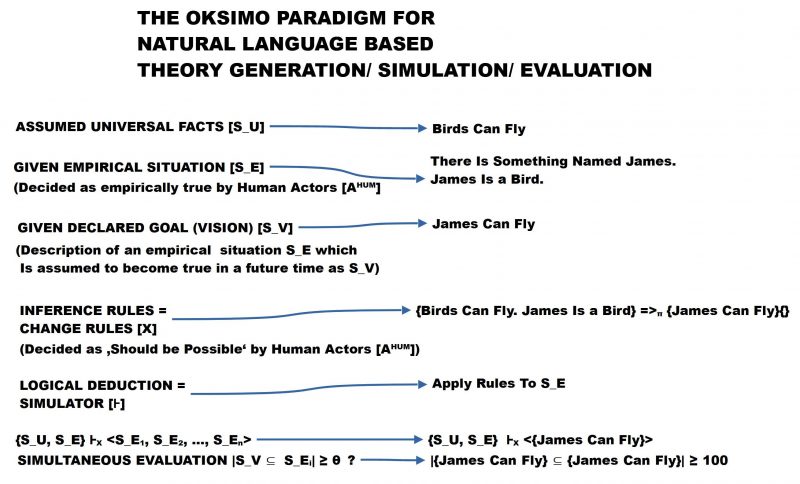
- I have started a ‘book project’ in parallel. This was motivated by the need to provide potential users of our new oksimo.R software with a coherent explanation of how the oksimo.R software, when used, generates an empirical theory in the format of a screenplay. The primary source of the book is in German and will be translated step by step here in the uffmm.blog.
INTRODUCTION
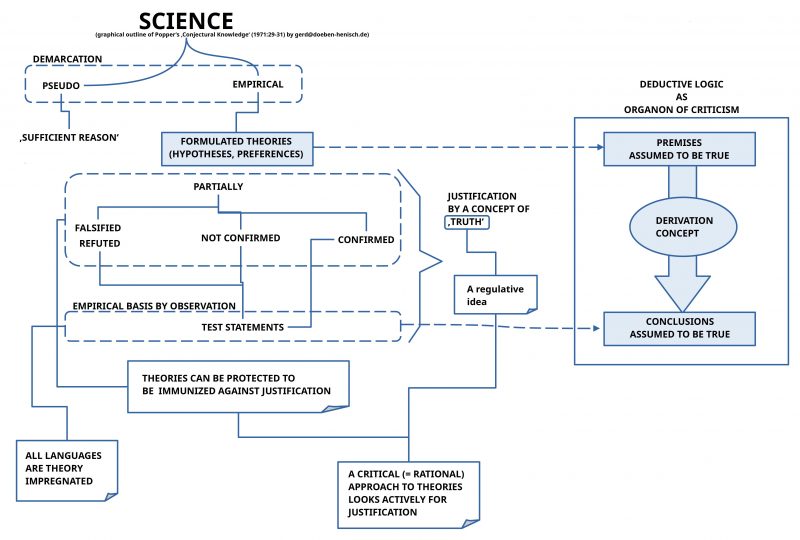
In a rather foundational paper about an idea, how one can generalize ‘systems engineering’ [*1] to the art of ‘theory engineering’ [1] a new conceptual framework has been outlined for a ‘sustainable applied empirical theory (SAET)’. Part of this new framework has been the idea that the classical recourse to groups of special experts (mostly ‘engineers’ in engineering) is too restrictive in the light of the new requirement of being sustainable: sustainability is primarily based on ‘diversity’ combined with the ‘ability to predict’ from this diversity probable future states which keep life alive. The aspect of diversity induces the challenge to see every citizen as a ‘natural expert’, because nobody can know in advance and from some non-existing absolut point of truth, which knowledge is really important. History shows that the ‘mainstream’ is usually to a large degree ‘biased’ [*1b].
With this assumption, that every citizen is a ‘natural expert’, science turns into a ‘general science’ where all citizens are ‘natural members’ of science. I will call this more general concept of science ‘sustainable citizen science (SCS)’ or ‘Citizen Science 2.0 (CS2)’. The important point here is that a sustainable citizen science is not necessarily an ‘arbitrary’ process. While the requirement of ‘diversity’ relates to possible contents, to possible ideas, to possible experiments, and the like, it follows from the other requirement of ‘predictability’/ of being able to make some useful ‘forecasts’, that the given knowledge has to be in a format, which allows in a transparent way the construction of some consequences, which ‘derive’ from the ‘given’ knowledge and enable some ‘new’ knowledge. This ability of forecasting has often been understood as the business of ‘logic’ providing an ‘inference concept’ given by ‘rules of deduction’ and a ‘practical pattern (on the meta level)’, which defines how these rules have to be applied to satisfy the inference concept. But, looking to real life, to everyday life or to modern engineering and economy, one can learn that ‘forecasting’ is a complex process including much more than only cognitive structures nicely fitting into some formulas. For this more realistic forecasting concept we will use here the wording ‘common logic’ and for the cognitive adventure where common logic is applied we will use the wording ‘common science’. ‘Common science’ is structurally not different from ‘usual science’, but it has a substantial wider scope and is using the whole of mankind as ‘experts’.
The following chapters/ sections try to illustrate this common science view by visiting different special views which all are only ‘parts of a whole’, a whole which we can ‘feel’ in every moment, but which we can not yet completely grasp with our theoretical concepts.
CONTENT
- Language (Main message: “The ordinary language is the ‘meta language’ to every special language. This can be used as a ‘hint’ to something really great: the mystery of the ‘self-creating’ power of the ordinary language which for most people is unknown although it happens every moment.”)
- Concrete Abstract Statements (Main message: “… you will probably detect, that nearly all words of a language are ‘abstract words’ activating ‘abstract meanings’. …If you cannot provide … ‘concrete situations’ the intended meaning of your abstract words will stay ‘unclear’: they can mean ‘nothing or all’, depending from the decoding of the hearer.”)
- True False Undefined (Main message: “… it reveals that ’empirical (observational) evidence’ is not necessarily an automatism: it presupposes appropriate meaning spaces embedded in sets of preferences, which are ‘observation friendly’.“
- Beyond Now (Main message: “With the aid of … sequences revealing possible changes the NOW is turned into a ‘moment’ embedded in a ‘process’, which is becoming the more important reality. The NOW is something, but the PROCESS is more.“)
- Playing with the Future (Main message: “In this sense seems ‘language’ to be the master tool for every brain to mediate its dynamic meaning structures with symbolic fix points (= words, expressions) which as such do not change, but the meaning is ‘free to change’ in any direction. And this ‘built in ‘dynamics’ represents an ‘internal potential’ for uncountable many possible states, which could perhaps become ‘true’ in some ‘future state’. Thus ‘future’ can begin in these potentials, and thinking is the ‘playground’ for possible futures.(but see [18])”)
- Forecasting – Prediction: What? (This chapter explains the cognitive machinery behind forecasting/ predictions, how groups of human actors can elaborate shared descriptions, and how it is possible to start with sequences of singularities to built up a growing picture of the empirical world which appears as a radical infinite and indeterministic space. )
- !!! From here all the following chapters have to be re-written !!!
- THE LOGIC OF EVERYDAY THINKING. Lets try an Example (Will probably be re-written too)
- Boolean Logic (Explains what boolean logic is, how it enables the working of programmable machines, but that it is of nearly no help for the ‘heart’ of forecasting.)
- … more re-writing will probably happen …
- Everyday Language: German Example
- Everyday Language: English
- Natural Logic
- Predicate Logic
- True Statements
- Formal Logic Inference: Preserving Truth
- Ordinary Language Inference: Preserving and Creating Truth
- Hidden Ontologies: Cognitively Real and Empirically Real
- AN INFERENCE IS NOT AUTOMATICALLY A FORECAST
- EMPIRICAL THEORY
- Side Trip to Wikipedia
- SUSTAINABLE EMPIRICAL THEORY
- CITIZEN SCIENCE 2.0
- … ???
COMMENTS
wkp-en := Englisch Wikipedia
/* Often people argue against the usage of the wikipedia encyclopedia as not ‘scientific’ because the ‘content’ of an entry in this encyclopedia can ‘change’. This presupposes the ‘classical view’ of scientific texts to be ‘stable’, which presupposes further, that such a ‘stable text’ describes some ‘stable subject matter’. But this view of ‘steadiness’ as the major property of ‘true descriptions’ is in no correspondence with real scientific texts! The reality of empirical science — even as in some special disciplines like ‘physics’ — is ‘change’. Looking to Aristotle’s view of nature, to Galileo Galilei, to Newton, to Einstein and many others, you will not find a ‘single steady picture’ of nature and science, and physics is only a very simple strand of science compared to the live-sciences and many others. Thus wikipedia is a real scientific encyclopedia give you the breath of world knowledge with all its strengths and limits at once. For another, more general argument, see In Favour for Wikipedia */
[*1] Meaning operator ‘…’ : In this text (and in nearly all other texts of this author) the ‘inverted comma’ is used quite heavily. In everyday language this is not common. In some special languages (theory of formal languages or in programming languages or in meta-logic) the inverted comma is used in some special way. In this text, which is primarily a philosophical text, the inverted comma sign is used as a ‘meta-language operator’ to raise the intention of the reader to be aware, that the ‘meaning’ of the word enclosed in the inverted commas is ‘text specific’: in everyday language usage the speaker uses a word and assumes tacitly that his ‘intended meaning’ will be understood by the hearer of his utterance as ‘it is’. And the speaker will adhere to his assumption until some hearer signals, that her understanding is different. That such a difference is signaled is quite normal, because the ‘meaning’ which is associated with a language expression can be diverse, and a decision, which one of these multiple possible meanings is the ‘intended one’ in a certain context is often a bit ‘arbitrary’. Thus, it can be — but must not — a meta-language strategy, to comment to the hearer (or here: the reader), that a certain expression in a communication is ‘intended’ with a special meaning which perhaps is not the commonly assumed one. Nevertheless, because the ‘common meaning’ is no ‘clear and sharp subject’, a ‘meaning operator’ with the inverted commas has also not a very sharp meaning. But in the ‘game of language’ it is more than nothing 🙂
[*1b] That the main stream ‘is biased’ is not an accident, not a ‘strange state’, not a ‘failure’, it is the ‘normal state’ based on the deeper structure how human actors are ‘built’ and ‘genetically’ and ‘cultural’ ‘programmed’. Thus the challenge to ‘survive’ as part of the ‘whole biosphere’ is not a ‘partial task’ to solve a single problem, but to solve in some sense the problem how to ‘shape the whole biosphere’ in a way, which enables a live in the universe for the time beyond that point where the sun is turning into a ‘red giant’ whereby life will be impossible on the planet earth (some billion years ahead)[22]. A remarkable text supporting this ‘complex view of sustainability’ can be found in Clark and Harvey, summarized at the end of the text. [23]
[*2] The meaning of the expression ‘normal’ is comparable to a wicked problem. In a certain sense we act in our everyday world ‘as if there exists some standard’ for what is assumed to be ‘normal’. Look for instance to houses, buildings: to a certain degree parts of a house have a ‘standard format’ assuming ‘normal people’. The whole traffic system, most parts of our ‘daily life’ are following certain ‘standards’ making ‘planning’ possible. But there exists a certain percentage of human persons which are ‘different’ compared to these introduced standards. We say that they have a ‘handicap’ compared to this assumed ‘standard’, but this so-called ‘standard’ is neither 100% true nor is the ‘given real world’ in its properties a ‘100% subject’. We have learned that ‘properties of the real world’ are distributed in a rather ‘statistical manner’ with different probabilities of occurrences. To ‘find our way’ in these varying occurrences we try to ‘mark’ the main occurrences as ‘normal’ to enable a basic structure for expectations and planning. Thus, if in this text the expression ‘normal’ is used it refers to the ‘most common occurrences’.
[*3] Thus we have here a ‘threefold structure’ embracing ‘perception events, memory events, and expression events’. Perception events represent ‘concrete events’; memory events represent all kinds of abstract events but they all have a ‘handle’ which maps to subsets of concrete events; expression events are parts of an abstract language system, which as such is dynamically mapped onto the abstract events. The main source for our knowledge about perceptions, memory and expressions is experimental psychology enhanced by many other disciplines.
[*4] Characterizing language expressions by meaning – the fate of any grammar: the sentence ” … ‘words’ (= expressions) of a language which can activate such abstract meanings are understood as ‘abstract words’, ‘general words’, ‘category words’ or the like.” is pointing to a deep property of every ordinary language, which represents the real power of language but at the same time the great weakness too: expressions as such have no meaning. Hundreds, thousands, millions of words arranged in ‘texts’, ‘documents’ can show some statistical patterns’ and as such these patterns can give some hint which expressions occur ‘how often’ and in ‘which combinations’, but they never can give a clue to the associated meaning(s). During more than three-thousand years humans have tried to describe ordinary language in a more systematic way called ‘grammar’. Due to this radically gap between ‘expressions’ as ‘observable empirical facts’ and ‘meaning constructs’ hidden inside the brain it was all the time a difficult job to ‘classify’ expressions as representing a certain ‘type’ of expression like ‘nouns’, ‘predicates’, ‘adjectives’, ‘defining article’ and the like. Without regressing to the assumed associated meaning such a classification is not possible. On account of the fuzziness of every meaning ‘sharp definitions’ of such ‘word classes’ was never and is not yet possible. One of the last big — perhaps the biggest ever — project of a complete systematic grammar of a language was the grammar project of the ‘Akademie der Wissenschaften der DDR’ (‘Academy of Sciences of the GDR’) from 1981 with the title “Grundzüge einer Deutschen Grammatik” (“Basic features of a German grammar”). A huge team of scientists worked together using many modern methods. But in the preface you can read, that many important properties of the language are still not sufficiently well describable and explainable. See: Karl Erich Heidolph, Walter Flämig, Wolfgang Motsch et al.: Grundzüge einer deutschen Grammatik. Akademie, Berlin 1981, 1028 Seiten.
[*5] Differing opinions about a given situation manifested in uttered expressions are a very common phenomenon in everyday communication. In some sense this is ‘natural’, can happen, and it should be no substantial problem to ‘solve the riddle of being different’. But as you can experience, the ability of people to solve the occurrence of different opinions is often quite weak. Culture is suffering by this as a whole.
[1] Gerd Doeben-Henisch, 2022, From SYSTEMS Engineering to THEORYEngineering, see: https://www.uffmm.org/2022/05/26/from-systems-engineering-to-theory-engineering/(Remark: At the time of citation this post was not yet finished, because there are other posts ‘corresponding’ with that post, which are too not finished. Knowledge is a dynamic network of interwoven views …).
[1d] ‘usual science’ is the game of science without having a sustainable format like in citizen science 2.0.
[2] Science, see e.g. wkp-en: https://en.wikipedia.org/wiki/Science
Citation = “Science is a systematic enterprise that builds and organizes knowledge in the form of testable explanations and predictions about the universe.[1][2]”
Citation = “In modern science, the term “theory” refers to scientific theories, a well-confirmed type of explanation of nature, made in a way consistent with the scientific method, and fulfilling the criteria required by modern science. Such theories are described in such a way that scientific tests should be able to provide empirical support for it, or empirical contradiction (“falsify“) of it. Scientific theories are the most reliable, rigorous, and comprehensive form of scientific knowledge,[1] in contrast to more common uses of the word “theory” that imply that something is unproven or speculative (which in formal terms is better characterized by the word hypothesis).[2] Scientific theories are distinguished from hypotheses, which are individual empirically testable conjectures, and from scientific laws, which are descriptive accounts of the way nature behaves under certain conditions.”
Citation = “New knowledge in science is advanced by research from scientists who are motivated by curiosity about the world and a desire to solve problems.[27][28] Contemporary scientific research is highly collaborative and is usually done by teams in academic and research institutions,[29] government agencies, and companies.[30][31] The practical impact of their work has led to the emergence of science policies that seek to influence the scientific enterprise by prioritizing the ethical and moral development of commercial products, armaments, health care, public infrastructure, and environmental protection.”
[2b] History of science in wkp-en: https://en.wikipedia.org/wiki/History_of_science#Scientific_Revolution_and_birth_of_New_Science
[3] Theory, see wkp-en: https://en.wikipedia.org/wiki/Theory#:~:text=A%20theory%20is%20a%20rational,or%20no%20discipline%20at%20all.
Citation = “A theory is a rational type of abstract thinking about a phenomenon, or the results of such thinking. The process of contemplative and rational thinking is often associated with such processes as observational study or research. Theories may be scientific, belong to a non-scientific discipline, or no discipline at all. Depending on the context, a theory’s assertions might, for example, include generalized explanations of how nature works. The word has its roots in ancient Greek, but in modern use it has taken on several related meanings.”
[4] Scientific theory, see: wkp-en: https://en.wikipedia.org/wiki/Scientific_theory
Citation = “In modern science, the term “theory” refers to scientific theories, a well-confirmed type of explanation of nature, made in a way consistent with the scientific method, and fulfilling the criteria required by modern science. Such theories are described in such a way that scientific tests should be able to provide empirical support for it, or empirical contradiction (“falsify“) of it. Scientific theories are the most reliable, rigorous, and comprehensive form of scientific knowledge,[1] in contrast to more common uses of the word “theory” that imply that something is unproven or speculative (which in formal terms is better characterized by the word hypothesis).[2] Scientific theories are distinguished from hypotheses, which are individual empirically testable conjectures, and from scientific laws, which are descriptive accounts of the way nature behaves under certain conditions.”
[4b] Empiricism in wkp-en: https://en.wikipedia.org/wiki/Empiricism
[4c] Scientific method in wkp-en: https://en.wikipedia.org/wiki/Scientific_method
Citation =”The scientific method is an empirical method of acquiring knowledge that has characterized the development of science since at least the 17th century (with notable practitioners in previous centuries). It involves careful observation, applying rigorous skepticism about what is observed, given that cognitive assumptions can distort how one interprets the observation. It involves formulating hypotheses, via induction, based on such observations; experimental and measurement-based statistical testing of deductions drawn from the hypotheses; and refinement (or elimination) of the hypotheses based on the experimental findings. These are principles of the scientific method, as distinguished from a definitive series of steps applicable to all scientific enterprises.[1][2][3] [4c]
and
Citation = “The purpose of an experiment is to determine whether observations[A][a][b] agree with or conflict with the expectations deduced from a hypothesis.[6]: Book I, [6.54] pp.372, 408 [b] Experiments can take place anywhere from a garage to a remote mountaintop to CERN’s Large Hadron Collider. There are difficulties in a formulaic statement of method, however. Though the scientific method is often presented as a fixed sequence of steps, it represents rather a set of general principles.[7] Not all steps take place in every scientific inquiry (nor to the same degree), and they are not always in the same order.[8][9]”
[5] Gerd Doeben-Henisch, “Is Mathematics a Fake? No! Discussing N.Bourbaki, Theory of Sets (1968) – Introduction”, 2022, https://www.uffmm.org/2022/06/06/n-bourbaki-theory-of-sets-1968-introduction/
[6] Logic, see wkp-en: https://en.wikipedia.org/wiki/Logic
[7] W. C. Kneale, The Development of Logic, Oxford University Press (1962)
[8] Set theory, in wkp-en: https://en.wikipedia.org/wiki/Set_theory
[9] N.Bourbaki, Theory of Sets , 1968, with a chapter about structures, see: https://en.wikipedia.org/wiki/%C3%89l%C3%A9ments_de_math%C3%A9matique
[10] = [5]
[11] Ludwig Josef Johann Wittgenstein ( 1889 – 1951): https://en.wikipedia.org/wiki/Ludwig_Wittgenstein
[12] Ludwig Wittgenstein, 1953: Philosophische Untersuchungen [PU], 1953: Philosophical Investigations [PI], translated by G. E. M. Anscombe /* For more details see: https://en.wikipedia.org/wiki/Philosophical_Investigations */
[13] Wikipedia EN, Speech acts: https://en.wikipedia.org/wiki/Speech_act
[14] While the world view constructed in a brain is ‘virtual’ compared to the ‘real word’ outside the brain (where the body outside the brain is also functioning as ‘real world’ in relation to the brain), does the ‘virtual world’ in the brain function for the brain mostly ‘as if it is the real world’. Only under certain conditions can the brain realize a ‘difference’ between the triggering outside real world and the ‘virtual substitute for the real world’: You want to use your bicycle ‘as usual’ and then suddenly you have to notice that it is not at that place where is ‘should be’. …
[15] Propositional Calculus, see wkp-en: https://en.wikipedia.org/wiki/Propositional_calculus#:~:text=Propositional%20calculus%20is%20a%20branch,of%20arguments%20based%20on%20them.
[16] Boolean algebra, see wkp-en: https://en.wikipedia.org/wiki/Boolean_algebra
[17] Boolean (or propositional) Logic: As one can see in the mentioned articles of the English wikipedia, the term ‘boolean logic’ is not common. The more logic-oriented authors prefer the term ‘boolean calculus’ [15] and the more math-oriented authors prefer the term ‘boolean algebra’ [16]. In the view of this author the general view is that of ‘language use’ with ‘logic inference’ as leading idea. Therefore the main topic is ‘logic’, in the case of propositional logic reduced to a simple calculus whose similarity with ‘normal language’ is widely ‘reduced’ to a play with abstract names and operators. Recommended: the historical comments in [15].
[18] Clearly, thinking alone can not necessarily induce a possible state which along the time line will become a ‘real state’. There are numerous factors ‘outside’ the individual thinking which are ‘driving forces’ to push real states to change. But thinking can in principle synchronize with other individual thinking and — in some cases — can get a ‘grip’ on real factors causing real changes.
[19] This kind of knowledge is not delivered by brain science alone but primarily from experimental (cognitive) psychology which examines observable behavior and ‘interprets’ this behavior with functional models within an empirical theory.
[20] Predicate Logic or First-Order Logic or … see: wkp-en: https://en.wikipedia.org/wiki/First-order_logic#:~:text=First%2Dorder%20logic%E2%80%94also%20known,%2C%20linguistics%2C%20and%20computer%20science.
[21] Gerd Doeben-Henisch, In Favour of Wikipedia, https://www.uffmm.org/2022/07/31/in-favour-of-wikipedia/, 31 July 2022
[22] The sun, see wkp-ed https://en.wikipedia.org/wiki/Sun (accessed 8 Aug 2022)
[23] By Clark, William C., and Alicia G. Harley – https://doi.org/10.1146/annurev-environ-012420-043621, Clark, William C., and Alicia G. Harley. 2020. “Sustainability Science: Toward a Synthesis.” Annual Review of Environment and Resources 45 (1): 331–86, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=109026069
[24] Sustainability in wkp-en: https://en.wikipedia.org/wiki/Sustainability#Dimensions_of_sustainability
[25] Sustainable Development in wkp-en: https://en.wikipedia.org/wiki/Sustainable_development
[26] Marope, P.T.M; Chakroun, B.; Holmes, K.P. (2015). Unleashing the Potential: Transforming Technical and Vocational Education and Training (PDF). UNESCO. pp. 9, 23, 25–26. ISBN978-92-3-100091-1.
[27] SDG 4 in wkp-en: https://en.wikipedia.org/wiki/Sustainable_Development_Goal_4
[28] Thomas Rid, Rise of the Machines. A Cybernetic History, W.W.Norton & Company, 2016, New York – London
[29] Doeben-Henisch, G., 2006, Reducing Negative Complexity by a Semiotic System In: Gudwin, R., & Queiroz, J., (Eds). Semiotics and Intelligent Systems Development. Hershey et al: Idea Group Publishing, 2006, pp.330-342
[30] Döben-Henisch, G., Reinforcing the global heartbeat: Introducing the planet earth simulator project, In M. Faßler & C. Terkowsky (Eds.), URBAN FICTIONS. Die Zukunft des Städtischen. München, Germany: Wilhelm Fink Verlag, 2006, pp.251-263
[29] The idea that individual disciplines are not good enough for the ‘whole of knowledge’ is expressed in a clear way in a video of the theoretical physicist and philosopher Carlo Rovell: Carlo Rovelli on physics and philosophy, June 1, 2022, Video from the Perimeter Institute for Theoretical Physics. Theoretical physicist, philosopher, and international bestselling author Carlo Rovelli joins Lauren and Colin for a conversation about the quest for quantum gravity, the importance of unlearning outdated ideas, and a very unique way to get out of a speeding ticket.
[] By Azote for Stockholm Resilience Centre, Stockholm University – https://www.stockholmresilience.org/research/research-news/2016-06-14-how-food-connects-all-the-sdgs.html, CC BY 4.0, https://commons.wikimedia.org/w/index.php?curid=112497386
[] Intergovernmental Science-Policy Platform on Biodiversity and Ecosystem Services (IPBES) in wkp-en, UTL: https://en.wikipedia.org/wiki/Intergovernmental_Science-Policy_Platform_on_Biodiversity_and_Ecosystem_Services
[] IPBES (2019): Global assessment report on biodiversity and ecosystem services of the Intergovernmental Science-Policy Platform on Biodiversity and Ecosystem Services. E. S. Brondizio, J. Settele, S. Díaz, and H. T. Ngo (editors). IPBES secretariat, Bonn, Germany. 1148 pages. https://doi.org/10.5281/zenodo.3831673
[] Michaelis, L. & Lorek, S. (2004). “Consumption and the Environment in Europe: Trends and Futures.” Danish Environmental Protection Agency. Environmental Project No. 904.
[] Pezzey, John C. V.; Michael A., Toman (2002). “The Economics of Sustainability: A Review of Journal Articles” (PDF). —. Archived from the original (PDF) on 8 April 2014. Retrieved 8 April 2014.
[] World Business Council for Sustainable Development (WBCSD) in wkp-en: https://en.wikipedia.org/wiki/World_Business_Council_for_Sustainable_Development
[] Sierra Club in wkp-en: https://en.wikipedia.org/wiki/Sierra_Club
[] Herbert Bruderer, Where is the Cradle of the Computer?, June 20, 2022, URL: https://cacm.acm.org/blogs/blog-cacm/262034-where-is-the-cradle-of-the-computer/fulltext (accessed: July 20, 2022)
[] UN. Secretary-General; World Commission on Environment and Development, 1987, Report of the World Commission on Environment and Development : note / by the Secretary-General., https://digitallibrary.un.org/record/139811 (accessed: July 20, 2022) (A more readable format: https://sustainabledevelopment.un.org/content/documents/5987our-common-future.pdf )
/* Comment: Gro Harlem Brundtland (Norway) has been the main coordinator of this document */
[] Chaudhuri, S.,et al.Neurosymbolic programming. Foundations and Trends in Programming Languages 7, 158-243 (2021).
[] Noam Chomsky, “A Review of B. F. Skinner’s Verbal Behavior”, in Language, 35, No. 1 (1959), 26-58.(Online: https://chomsky.info/1967____/, accessed: July 21, 2022)
[] Churchman, C. West (December 1967). “Wicked Problems”. Management Science. 14 (4): B-141–B-146. doi:10.1287/mnsc.14.4.B141.
[-] Yen-Chia Hsu, Illah Nourbakhsh, “When Human-Computer Interaction Meets Community Citizen Science“,Communications of the ACM, February 2020, Vol. 63 No. 2, Pages 31-34, 10.1145/3376892, https://cacm.acm.org/magazines/2020/2/242344-when-human-computer-interaction-meets-community-citizen-science/fulltext
[] Yen-Chia Hsu, Ting-Hao ‘Kenneth’ Huang, Himanshu Verma, Andrea Mauri, Illah Nourbakhsh, Alessandro Bozzon, Empowering local communities using artificial intelligence, DOI:https://doi.org/10.1016/j.patter.2022.100449, CellPress, Patterns, VOLUME 3, ISSUE 3, 100449, MARCH 11, 2022
[] Nello Cristianini, Teresa Scantamburlo, James Ladyman, The social turn of artificial intelligence, in: AI & SOCIETY, https://doi.org/10.1007/s00146-021-01289-8
[] Carl DiSalvo, Phoebe Sengers, and Hrönn Brynjarsdóttir, Mapping the landscape of sustainable hci, In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems, CHI ’10, page 1975–1984, New York, NY, USA, 2010. Association for Computing Machinery.
[] Claude Draude, Christian Gruhl, Gerrit Hornung, Jonathan Kropf, Jörn Lamla, Jan Marco Leimeister, Bernhard Sick, Gerd Stumme, Social Machines, in: Informatik Spektrum, https://doi.org/10.1007/s00287-021-01421-4
[] EU: High-Level Expert Group on AI (AI HLEG), A definition of AI: Main capabilities and scientific disciplines, European Commission communications published on 25 April 2018 (COM(2018) 237 final), 7 December 2018 (COM(2018) 795 final) and 8 April 2019 (COM(2019) 168 final). For our definition of Artificial Intelligence (AI), please refer to our document published on 8 April 2019: https://ec.europa.eu/newsroom/dae/document.cfm?doc_id=56341
[] EU: High-Level Expert Group on AI (AI HLEG), Policy and investment recommendations for trustworthy Artificial Intelligence, 2019, https://digital-strategy.ec.europa.eu/en/library/policy-and-investment-recommendations-trustworthy-artificial-intelligence
[] European Union. Regulation 2016/679 of the European Parliament and of the Council of 27 April 2016 on the protection of natural persons with regard to the processing of personal data and on the free movement of such data, and repealing Directive 95/46/EC General Data Protection Regulation; http://eur-lex.europa.eu/eli/reg/2016/679/oj (Wirksam ab 25.Mai 2018) [26.2.2022]
[] C.S. Holling. Resilience and stability of ecological systems. Annual Review of Ecology and Systematics, 4(1):1–23, 1973
[] John P. van Gigch. 1991. System Design Modeling and Metamodeling. Springer US. DOI:https://doi.org/10.1007/978-1-4899-0676-2
[] Gudwin, R.R. (2002), Semiotic Synthesis and Semionic Networks, S.E.E.D. Journal (Semiotics, Energy, Evolution, Development), Volume 2, No.2, pp.55-83.
[] Gudwin, R.R. (2003), On a Computational Model of the Peircean Semiosis, IEEE KIMAS 2003 Proceedings
[] J.A. Jacko and A. Sears, Eds., The Human-Computer Interaction Handbook. Fundamentals, Evolving Technologies, and emerging Applications. 1st edition, 2003.
[] LeCun, Y., Bengio, Y., & Hinton, G. Deep learning. Nature 521, 436-444 (2015).
[] Lenat, D. What AI can learn from Romeo & Juliet.Forbes (2019)
[] Pierre Lévy, Collective Intelligence. mankind’s emerging world in cyberspace, Perseus books, Cambridge (M A), 1997 (translated from the French Edition 1994 by Robert Bonnono)
[] Lexikon der Nachhaltigkeit, ‘Starke Nachhaltigkeit‘, https://www.nachhaltigkeit.info/artikel/schwache_vs_starke_nachhaltigkeit_1687.htm (acessed: July 21, 2022)
[] Michael L. Littman, Ifeoma Ajunwa, Guy Berger, Craig Boutilier, Morgan Currie, Finale Doshi-Velez, Gillian Hadfield, Michael C. Horowitz, Charles Isbell, Hiroaki Kitano, Karen Levy, Terah Lyons, Melanie Mitchell, Julie Shah, Steven Sloman, Shannon Vallor, and Toby Walsh. “Gathering Strength, Gathering Storms: The One Hundred Year Study on Artificial Intelligence (AI100) 2021 Study Panel Report.” Stanford University, Stanford, CA, September 2021. Doc: http://ai100.stanford.edu/2021-report.
[] Markus Luczak-Roesch, Kieron O’Hara, Ramine Tinati, Nigel Shadbolt, Socio-technical Computation, CSCW’15 Companion, March 14–18, 2015, Vancouver, BC, Canada, ACM 978-1-4503-2946-0/15/03, http://dx.doi.org/10.1145/2685553.2698991
[] Marcus, G.F., et al. Overregularization in language acquisition. Monographs of the Society for Research in Child Development 57 (1998).
[] Gary Marcus and Ernest Davis, Rebooting AI, Published by Pantheon,
Sep 10, 2019, 288 Pages
[] Gary Marcus, Deep Learning Is Hitting a Wall. What would it take for artificial intelligence to make real progress, March 10, 2022, URL: https://nautil.us/deep-learning-is-hitting-a-wall-14467/ (accessed: July 20, 2022)
[] Kathryn Merrick. Value systems for developmental cognitive robotics: A survey. Cognitive Systems Research, 41:38 – 55, 2017
[] Illah Reza Nourbakhsh and Jennifer Keating, AI and Humanity, MIT Press, 2020 /* An examination of the implications for society of rapidly advancing artificial intelligence systems, combining a humanities perspective with technical analysis; includes exercises and discussion questions. */
[] Olazaran, M. , A sociological history of the neural network controversy. Advances in Computers 37, 335-425 (1993).
[] Friedrich August Hayek (1945), The use of knowledge in society. The American Economic Review 35, 4 (1945), 519–530
[] Karl Popper, „A World of Propensities“, in: Karl Popper, „A World of Propensities“, Thoemmes Press, Bristol, (Vortrag 1988, leicht erweitert neu abgedruckt 1990, repr. 1995)
[] Karl Popper, „Towards an Evolutionary Theory of Knowledge“, in: Karl Popper, „A World of Propensities“, Thoemmes Press, Bristol, (Vortrag 1989, ab gedruckt in 1990, repr. 1995)
[] Karl Popper, „All Life is Problem Solving“, Artikel, ursprünglich ein Vortrag 1991 auf Deutsch, erstmalig publiziert in dem Buch (auf Deutsch) „Alles Leben ist Problemlösen“ (1994), dann in dem Buch (auf Englisch) „All Life is Problem Solving“, 1999, Routledge, Taylor & Francis Group, London – New York
[] Rittel, Horst W.J.; Webber, Melvin M. (1973). “Dilemmas in a General Theory of Planning” (PDF). Policy Sciences. 4 (2): 155–169. doi:10.1007/bf01405730. S2CID 18634229. Archived from the original (PDF) on 30 September 2007. [Reprinted in Cross, N., ed. (1984). Developments in Design Methodology. Chichester, England: John Wiley & Sons. pp. 135–144.]
[] Ritchey, Tom (2013) [2005]. “Wicked Problems: Modelling Social Messes with Morphological Analysis”. Acta Morphologica Generalis. 2 (1). ISSN 2001-2241. Retrieved 7 October 2017.
[] Stuart Russell and Peter Norvig, Artificial Intelligence: A Modern Approach, 4th US ed., 2021, URL: http://aima.cs.berkeley.edu/index.html (accessed: July 20, 2022)
[] A. Sears and J.A. Jacko, Eds., The Human-Computer Interaction Handbook. Fundamentals, Evolving Technologies, and emerging Applications. 2nd edition, 2008.
[] Skaburskis, Andrejs (19 December 2008). “The origin of “wicked problems””. Planning Theory & Practice. 9 (2): 277-280. doi:10.1080/14649350802041654. At the end of Rittel’s presentation, West Churchman responded with that pensive but expressive movement of voice that some may well remember, ‘Hmm, those sound like “wicked problems.”‘
[] Tonkinwise, Cameron (4 April 2015). “Design for Transitions – from and to what?”. Academia.edu. Retrieved 9 November 2017.
[] Thoppilan, R., et al. LaMDA: Language models for dialog applications. arXiv 2201.08239 (2022).
[] Wurm, Daniel; Zielinski, Oliver; Lübben, Neeske; Jansen, Maike; Ramesohl,
Stephan (2021) : Wege in eine ökologische Machine Economy: Wir brauchen eine ‘Grüne Governance der Machine Economy’, um das Zusammenspiel von Internet of Things, Künstlicher Intelligenz und Distributed Ledger Technology ökologisch zu gestalten, Wuppertal Report, No. 22, Wuppertal Institut für Klima, Umwelt, Energie, Wuppertal, https://doi.org/10.48506/opus-7828
[] Aimee van Wynsberghe, Sustainable AI: AI for sustainability and the sustainability of AI, in: AI and Ethics (2021) 1:213–218, see: https://doi.org/10.1007/s43681
[-] Sarah West, Rachel Pateman, 2017, “How could citizen science support the Sustainable Development Goals?“, SEI Stockholm Environment Institut , 2017, see: https://mediamanager.sei.org/documents/Publications/SEI-2017-PB-citizen-science-sdgs.pdf
[] R. I. Damper (2000), Editorial for the special issue on ‘Emergent Properties of Complex Systems’: Emergence and levels of abstraction. International Journal of Systems Science 31, 7 (2000), 811–818. DOI:https://doi.org/10.1080/002077200406543
[] Gerd Doeben-Henisch (2004), The Planet Earth Simulator Project – A Case Study in Computational Semiotics, IEEE AFRICON 2004, pp.417 – 422
[] Boder, A. (2006), “Collective intelligence: a keystone in knowledge management”, Journal of Knowledge Management, Vol. 10 No. 1, pp. 81-93. https://doi.org/10.1108/13673270610650120
[] Wikipedia, ‘Weak and strong sustainability’, https://en.wikipedia.org/wiki/Weak_and_strong_sustainability (accessed: July 21, 2022)
[] Florence Maraninchi, Let us Not Put All Our Eggs in One Basket. Towards new research directions in computer Science, CACM Communications of the ACM, September 2022, Vol.65, No.9, pp.35-37, https://dl.acm.org/doi/10.1145/3528088
[] AYA H. KIMURA and ABBY KINCHY, “Citizen Science: Probing the Virtues and Contexts of Participatory Research”, Engaging Science, Technology, and Society 2 (2016), 331-361, DOI:10.17351/ests2016.099
[] Eric Bonabeau (2009), Decisions 2.0: The power of collective intelligence. MIT Sloan Management Review 50, 2 (Winter 2009), 45-52.
[] Jim Giles (2005), Internet encyclopaedias go head to head. Nature 438, 7070 (Dec. 2005), 900–901. DOI:https://doi.org/10.1038/438900a
[] T. Bosse, C. M. Jonker, M. C. Schut, and J. Treur (2006), Collective representational content for shared extended mind. Cognitive Systems Research 7, 2-3 (2006), pp.151-174, DOI:https://doi.org/10.1016/j.cogsys.2005.11.007
[] Romina Cachia, Ramón Compañó, and Olivier Da Costa (2007), Grasping the potential of online social networks for foresight. Technological Forecasting and Social Change 74, 8 (2007), oo.1179-1203. DOI:https://doi.org/10.1016/j.techfore.2007.05.006
[] Tom Gruber (2008), Collective knowledge systems: Where the social web meets the semantic web. Web Semantics: Science, Services and Agents on the World Wide Web 6, 1 (2008), 4–13. DOI:https://doi.org/10.1016/j.websem.2007.11.011
[] Luca Iandoli, Mark Klein, and Giuseppe Zollo (2009), Enabling on-line deliberation and collective decision-making through large-scale argumentation. International Journal of Decision Support System Technology 1, 1 (Jan. 2009), 69–92. DOI:https://doi.org/10.4018/jdsst.2009010105
[] Shuangling Luo, Haoxiang Xia, Taketoshi Yoshida, and Zhongtuo Wang (2009), Toward collective intelligence of online communities: A primitive conceptual model. Journal of Systems Science and Systems Engineering 18, 2 (01 June 2009), 203–221. DOI:https://doi.org/10.1007/s11518-009-5095-0
[] Dawn G. Gregg (2010), Designing for collective intelligence. Communications of the ACM 53, 4 (April 2010), 134–138. DOI:https://doi.org/10.1145/1721654.1721691
[] Rolf Pfeifer, Jan Henrik Sieg, Thierry Bücheler, and Rudolf Marcel Füchslin. 2010. Crowdsourcing, open innovation and collective intelligence in the scientific method: A research agenda and operational framework. (2010). DOI:https://doi.org/10.21256/zhaw-4094
[] Martijn C. Schut. 2010. On model design for simulation of collective intelligence. Information Sciences 180, 1 (2010), 132–155. DOI:https://doi.org/10.1016/j.ins.2009.08.006 Special Issue on Collective Intelligence
[] Dimitrios J. Vergados, Ioanna Lykourentzou, and Epaminondas Kapetanios (2010), A resource allocation framework for collective intelligence system engineering. In Proceedings of the International Conference on Management of Emergent Digital EcoSystems (MEDES’10). ACM, New York, NY, 182–188. DOI:https://doi.org/10.1145/1936254.1936285
[] Anita Williams Woolley, Christopher F. Chabris, Alex Pentland, Nada Hashmi, and Thomas W. Malone (2010), Evidence for a collective intelligence factor in the performance of human groups. Science 330, 6004 (2010), 686–688. DOI:https://doi.org/10.1126/science.1193147
[] Michael A. Woodley and Edward Bell (2011), Is collective intelligence (mostly) the General Factor of Personality? A comment on Woolley, Chabris, Pentland, Hashmi and Malone (2010). Intelligence 39, 2 (2011), 79–81. DOI:https://doi.org/10.1016/j.intell.2011.01.004
[] Joshua Introne, Robert Laubacher, Gary Olson, and Thomas Malone (2011), The climate CoLab: Large scale model-based collaborative planning. In Proceedings of the 2011 International Conference on Collaboration Technologies and Systems (CTS’11). 40–47. DOI:https://doi.org/10.1109/CTS.2011.5928663
[] Miguel de Castro Neto and Ana Espírtio Santo (2012), Emerging collective intelligence business models. In MCIS 2012 Proceedings. Mediterranean Conference on Information Systems. https://aisel.aisnet.org/mcis2012/14
[] Peng Liu, Zhizhong Li (2012), Task complexity: A review and conceptualization framework, International Journal of Industrial Ergonomics 42 (2012), pp. 553 – 568
[] Sean Wise, Robert A. Paton, and Thomas Gegenhuber. (2012), Value co-creation through collective intelligence in the public sector: A review of US and European initiatives. VINE 42, 2 (2012), 251–276. DOI:https://doi.org/10.1108/03055721211227273
[] Antonietta Grasso and Gregorio Convertino (2012), Collective intelligence in organizations: Tools and studies. Computer Supported Cooperative Work (CSCW) 21, 4 (01 Oct 2012), 357–369. DOI:https://doi.org/10.1007/s10606-012-9165-3
[] Sandro Georgi and Reinhard Jung (2012), Collective intelligence model: How to describe collective intelligence. In Advances in Intelligent and Soft Computing. Vol. 113. Springer, 53–64. DOI:https://doi.org/10.1007/978-3-642-25321-8_5
[] H. Santos, L. Ayres, C. Caminha, and V. Furtado (2012), Open government and citizen participation in law enforcement via crowd mapping. IEEE Intelligent Systems 27 (2012), 63–69. DOI:https://doi.org/10.1109/MIS.2012.80
[] Jörg Schatzmann & René Schäfer & Frederik Eichelbaum (2013), Foresight 2.0 – Definition, overview & evaluation, Eur J Futures Res (2013) 1:15
DOI 10.1007/s40309-013-0015-4
[] Sylvia Ann Hewlett, Melinda Marshall, and Laura Sherbin (2013), How diversity can drive innovation. Harvard Business Review 91, 12 (2013), 30–30
[] Tony Diggle (2013), Water: How collective intelligence initiatives can address this challenge. Foresight 15, 5 (2013), 342–353. DOI:https://doi.org/10.1108/FS-05-2012-0032
[] Hélène Landemore and Jon Elster. 2012. Collective Wisdom: Principles and Mechanisms. Cambridge University Press. DOI:https://doi.org/10.1017/CBO9780511846427
[] Jerome C. Glenn (2013), Collective intelligence and an application by the millennium project. World Futures Review 5, 3 (2013), 235–243. DOI:https://doi.org/10.1177/1946756713497331
[] Detlef Schoder, Peter A. Gloor, and Panagiotis Takis Metaxas (2013), Social media and collective intelligence—Ongoing and future research streams. KI – Künstliche Intelligenz 27, 1 (1 Feb. 2013), 9–15. DOI:https://doi.org/10.1007/s13218-012-0228-x
[] V. Singh, G. Singh, and S. Pande (2013), Emergence, self-organization and collective intelligence—Modeling the dynamics of complex collectives in social and organizational settings. In 2013 UKSim 15th International Conference on Computer Modelling and Simulation. 182–189. DOI:https://doi.org/10.1109/UKSim.2013.77
[] A. Kornrumpf and U. Baumöl (2014), A design science approach to collective intelligence systems. In 2014 47th Hawaii International Conference on System Sciences. 361–370. DOI:https://doi.org/10.1109/HICSS.2014.53
[] Michael A. Peters and Richard Heraud. 2015. Toward a political theory of social innovation: Collective intelligence and the co-creation of social goods. 3, 3 (2015), 7–23. https://researchcommons.waikato.ac.nz/handle/10289/9569
[] Juho Salminen. 2015. The Role of Collective Intelligence in Crowdsourcing Innovation. PhD dissertation. Lappeenranta University of Technology
[] Aelita Skarzauskiene and Monika Maciuliene (2015), Modelling the index of collective intelligence in online community projects. In International Conference on Cyber Warfare and Security. Academic Conferences International Limited, 313
[] AYA H. KIMURA and ABBY KINCHY (2016), Citizen Science: Probing the Virtues and Contexts of Participatory Research, Engaging Science, Technology, and Society 2 (2016), 331-361, DOI:10.17351/ests2016.099
[] Philip Tetlow, Dinesh Garg, Leigh Chase, Mark Mattingley-Scott, Nicholas Bronn, Kugendran Naidoo†, Emil Reinert (2022), Towards a Semantic Information Theory (Introducing Quantum Corollas), arXiv:2201.05478v1 [cs.IT] 14 Jan 2022, 28 pages
[] Melanie Mitchell, What Does It Mean to Align AI With Human Values?, quanta magazin, Quantized Columns, 19.Devember 2022, https://www.quantamagazine.org/what-does-it-mean-to-align-ai-with-human-values-20221213#
Comment by Gerd Doeben-Henisch:
[] Nick Bostrom. Superintelligence. Paths, Dangers, Strategies. Oxford University Press, Oxford (UK), 1 edition, 2014.
[] Scott Aaronson, Reform AI Alignment, Update: 22.November 2022, https://scottaaronson.blog/?p=6821
[] Andrew Y. Ng, Stuart J. Russell, Algorithms for Inverse Reinforcement Learning, ICML 2000: Proceedings of the Seventeenth International Conference on Machine LearningJune 2000 Pages 663–670
[] Pat Langley (ed.), ICML ’00: Proceedings of the Seventeenth International Conference on Machine Learning, Morgan Kaufmann Publishers Inc., 340 Pine Street, Sixth Floor, San Francisco, CA, United States, Conference 29 June 2000- 2 July 2000, 29.June 2000
[] Daniel S. Brown, Wonjoon Goo, Prabhat Nagarajan, Scott Niekum, (2019) Extrapolating Beyond Suboptimal Demonstrations via
Inverse Reinforcement Learning from Observations, Proceedings of the 36 th International Conference on Machine Learning, Long Beach, California, PMLR 97, 2019. Copyright 2019 by the author(s): https://arxiv.org/pdf/1904.06387.pdf
Abstract: Extrapolating Beyond Suboptimal Demonstrations via
Inverse Reinforcement Learning from Observations
Daniel S. Brown * 1 Wonjoon Goo * 1 Prabhat Nagarajan 2 Scott Niekum 1
You can read in the abstract:
“A critical flaw of existing inverse reinforcement learning (IRL) methods is their inability to significantly outperform the demonstrator. This is because IRL typically seeks a reward function that makes the demonstrator appear near-optimal, rather than inferring the underlying intentions of the demonstrator that may have been poorly executed in practice. In this paper, we introduce
a novel reward-learning-from-observation algorithm, Trajectory-ranked Reward EXtrapolation (T-REX), that extrapolates beyond a set of (ap-
proximately) ranked demonstrations in order to infer high-quality reward functions from a set of potentially poor demonstrations. When combined
with deep reinforcement learning, T-REX outperforms state-of-the-art imitation learning and IRL methods on multiple Atari and MuJoCo bench-
mark tasks and achieves performance that is often more than twice the performance of the best demonstration. We also demonstrate that T-REX
is robust to ranking noise and can accurately extrapolate intention by simply watching a learner noisily improve at a task over time.”
[] Paul Christiano, Jan Leike, Tom B. Brown, Miljan Martic, Shane Legg, Dario Amodei, (2017), Deep reinforcement learning from human preferences, https://arxiv.org/abs/1706.03741
In the abstract you can read: “For sophisticated reinforcement learning (RL) systems to interact usefully with real-world environments, we need to communicate complex goals to these systems. In this work, we explore goals defined in terms of (non-expert) human preferences between pairs of trajectory segments. We show that this approach can effectively solve complex RL tasks without access to the reward function, including Atari games and simulated robot locomotion, while providing feedback on less than one percent of our agent’s interactions with the environment. This reduces the cost of human oversight far enough that it can be practically applied to state-of-the-art RL systems. To demonstrate the flexibility of our approach, we show that we can successfully train complex novel behaviors with about an hour of human time. These behaviors and environments are considerably more complex than any that have been previously learned from human feedback.
[] Melanie Mitchell,(2021), Abstraction and Analogy-Making in Artificial
Intelligence, https://arxiv.org/pdf/2102.10717.pdf
In the abstract you can read: “Conceptual abstraction and analogy-making are key abilities underlying humans’ abilities to learn, reason, and robustly adapt their knowledge to new domains. Despite of a long history of research on constructing AI systems with these abilities, no current AI system is anywhere close to a capability of forming humanlike abstractions or analogies. This paper reviews the advantages and limitations of several approaches toward this goal, including symbolic methods, deep learning, and probabilistic program induction. The paper concludes with several proposals for designing
challenge tasks and evaluation measures in order to make quantifiable and generalizable progress
[] Melanie Mitchell, (2021), Why AI is Harder Than We Think, https://arxiv.org/pdf/2102.10717.pdf
In the abstract you can read: “Since its beginning in the 1950s, the field of artificial intelligence has cycled several times between periods of optimistic predictions and massive investment (“AI spring”) and periods of disappointment, loss of confidence, and reduced funding (“AI winter”). Even with today’s seemingly fast pace of AI breakthroughs, the development of long-promised technologies such as self-driving cars, housekeeping robots, and conversational companions has turned out to be much harder than many people expected. One reason for these repeating cycles is our limited understanding of the nature and complexity of intelligence itself. In this paper I describe four fallacies in common assumptions made by AI researchers, which can lead to overconfident predictions about the field. I conclude by discussing the open questions spurred by these fallacies, including the age-old challenge of imbuing machines with humanlike common sense.”
[] Stuart Russell, (2019), Human Compatible: AI and the Problem of Control, Penguin books, Allen Lane; 1. Edition (8. Oktober 2019)
In the preface you can read: “This book is about the past , present , and future of our attempt to understand and create intelligence . This matters , not because AI is rapidly becoming a pervasive aspect of the present but because it is the dominant technology of the future . The world’s great powers are waking up to this fact , and the world’s largest corporations have known it for some time . We cannot predict exactly how the technology will develop or on what timeline . Nevertheless , we must plan for the possibility that machines will far exceed the human capacity for decision making in the real world . What then ? Everything civilization has to offer is the product of our intelligence ; gaining access to considerably greater intelligence would be the biggest event in human history . The purpose of the book is to explain why it might be the last event in human history and how to make sure that it is not .”
[] David Adkins, Bilal Alsallakh, Adeel Cheema, Narine Kokhlikyan, Emily McReynolds, Pushkar Mishra, Chavez Procope, Jeremy Sawruk, Erin Wang, Polina Zvyagina, (2022), Method Cards for Prescriptive Machine-Learning Transparency, 2022 IEEE/ACM 1st International Conference on AI Engineering – Software Engineering for AI (CAIN), CAIN’22, May 16–24, 2022, Pittsburgh, PA, USA, pp. 90 – 100, Association for Computing Machinery, ACM ISBN 978-1-4503-9275-4/22/05, New York, NY, USA, https://doi.org/10.1145/3522664.3528600
In the abstract you can read: “Specialized documentation techniques have been developed to communicate key facts about machine-learning (ML) systems and the datasets and models they rely on. Techniques such as Datasheets,
AI FactSheets, and Model Cards have taken a mainly descriptive
approach, providing various details about the system components.
While the above information is essential for product developers
and external experts to assess whether the ML system meets their
requirements, other stakeholders might find it less actionable. In
particular, ML engineers need guidance on how to mitigate po-
tential shortcomings in order to fix bugs or improve the system’s
performance. We propose a documentation artifact that aims to
provide such guidance in a prescriptive way. Our proposal, called
Method Cards, aims to increase the transparency and reproducibil-
ity of ML systems by allowing stakeholders to reproduce the models,
understand the rationale behind their designs, and introduce adap-
tations in an informed way. We showcase our proposal with an
example in small object detection, and demonstrate how Method
Cards can communicate key considerations that help increase the
transparency and reproducibility of the detection model. We fur-
ther highlight avenues for improving the user experience of ML
engineers based on Method Cards.”
[] John H. Miller, (2022), Ex Machina: Coevolving Machines and the Origins of the Social Universe, The SFI Press Scholars Series, 410 pages
Paperback ISBN: 978-1947864429 , DOI: 10.37911/9781947864429
In the announcement of the book you can read: “If we could rewind the tape of the Earth’s deep history back to the beginning and start the world anew—would social behavior arise yet again? While the study of origins is foundational to many scientific fields, such as physics and biology, it has rarely been pursued in the social sciences. Yet knowledge of something’s origins often gives us new insights into the present. In Ex Machina, John H. Miller introduces a methodology for exploring systems of adaptive, interacting, choice-making agents, and uses this approach to identify conditions sufficient for the emergence of social behavior. Miller combines ideas from biology, computation, game theory, and the social sciences to evolve a set of interacting automata from asocial to social behavior. Readers will learn how systems of simple adaptive agents—seemingly locked into an asocial morass—can be rapidly transformed into a bountiful social world driven only by a series of small evolutionary changes. Such unexpected revolutions by evolution may provide an important clue to the emergence of social life.”
[] Stefani A. Crabtree, Global Environmental Change, https://doi.org/10.1016/j.gloenvcha.2022.102597
In the abstract you can read: “Analyzing the spatial and temporal properties of information flow with a multi-century perspective could illuminate the sustainability of human resource-use strategies. This paper uses historical and archaeological datasets to assess how spatial, temporal, cognitive, and cultural limitations impact the generation and flow of information about ecosystems within past societies, and thus lead to tradeoffs in sustainable practices. While it is well understood that conflicting priorities can inhibit successful outcomes, case studies from Eastern Polynesia, the North Atlantic, and the American Southwest suggest that imperfect information can also be a major impediment
to sustainability. We formally develop a conceptual model of Environmental Information Flow and Perception (EnIFPe) to examine the scale of information flow to a society and the quality of the information needed to promote sustainable coupled natural-human systems. In our case studies, we assess key aspects of information flow by focusing on food web relationships and nutrient flows in socio-ecological systems, as well as the life cycles, population dynamics, and seasonal rhythms of organisms, the patterns and timing of species’ migration, and the trajectories of human-induced environmental change. We argue that the spatial and temporal dimensions of human environments shape society’s ability to wield information, while acknowledging that varied cultural factors also focus a society’s ability to act on such information. Our analyses demonstrate the analytical importance of completed experiments from the past, and their utility for contemporary debates concerning managing imperfect information and addressing conflicting priorities in modern environmental management and resource use.”