eJournal: uffmm.org, ISSN 2567-6458,
6.June 2022 – 13.June 2022, 10:30h
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de

SCOPE

In the uffmm review section the different papers and books are discussed from the point of view of the oksimo paradigm, which is embedded in the general view of a generalized ‘citizen science’ as a ‘computer aided sustainable applied empirical theory’ (CSAET). In the following text the author discusses the introduction of the book “Theory of Sets” from the series “Elements of Mathematics” by N.Bourbaki (1968) [1b]

CONTEXT

In the foundational post with the title “From SYSTEMS Engineering to THEORY Engineering” [3] the assumptions of the whole formalization approach in logic, mathematics and science are questioned as to narrow to allow a modern sustainable theory of science dealing explicitly with the future. To sharpen some of the arguments in that post it seems to be helpful to discuss one of the cornerstones of modern (formalized) mathematics substantiated in the book ‘Theory of sets’ from the Bourbaki group.[1a] It has to be mentioned that the question of the insufficiency of formalization has been discussed in the uffmm blog in several posts before. (cf. e.g. [2])

Formalization

preface

In the introduction to the ‘Set Theory Book’ the bourbaki group reveals a little bit of their meta-mathematical point of view, which finally belongs to the perspective of philosophy. At the one hand they try to be ‘radically formal’, but doing this they notice themselves that this is — by several reasons — only a ‘regulative idea’, somehow important for our thinking, but not completely feasible. This ‘practical impossibility’ is not necessarily a problem as long as one is conscious about this. The Bourbaki group is conscious about this problem, but different to their ‘rigor’ with the specialized formalization of mathematical ideas, they leave it widely ‘undefined’ what follows from the practical impossibility of being ‘completely rigorous’. In the following text it will be tried to describe the Bourbaki position with both dimensions: the idea of ‘formalization’ and the reality of ‘non-formalized realities’ which give the ‘ground’ for everything, even for the formalization. Doing this it will — hopefully — become clear that the idea of formalization was a great achievement in the philosophical and scientific thinking but it did not really solve our problems of understanding the world. The most important aspects of knowledge are ‘outside’ of this formalization approach, and many ‘problems’ which seem to bother our actual thinking are perhaps only ‘artifacts’ of this simplified formalization approach (somehow similar to the problems which have been induced by the metaphysical thinking of the older philosophy). To say it flatly: to introduce new names for old problems does not necessarily solve problems. It enables new ways of speaking and perhaps some new kinds of knowledge, but it does not really solve the big problems of knowledge. And the biggest problem of knowledge is — perhaps — the primary ‘knowledge machine’ itself: the biological actors which have brains to transform ‘reality’ in ‘virtual models’ in their brains and communication tools to ‘communicate’ these virtual models to enable a ‘collective intelligence’ as well as a ‘collective cooperation’. As long as we do not understand this we do not really understand the ‘process of knowing’.

before formalization

With the advent of the homo sapiens population on the planet earth about 300.000 years ago [4] it became possible that biological systems could transform their perceptions of the reality around their brains into ‘internal’, ‘virtual’ models, which enabled ‘reference points’ for ‘acting’ and a ‘cooperation’ which was synchronized by a ‘symbolic communication’. Those properties of the internal virtual models which have no clear ‘correspondence’ to the ‘reality between the brains’ are difficult to communicate.

Everyday symbolic communication refers to parts of the reality by certain types of expressions, which are ‘combined’ in manners which encode different types of ‘relations’ or even ‘changes’. Expressions which ‘refer’ to ‘concrete’ properties can be ‘overloaded’ by expressions which refer to other expressions, which in turn refer either again to expressions or to ‘concrete meanings’. Those objects which are the targets of a referring relation — concrete objects or other expressions — are here called ‘the meaning’ of the expressions. Thus the ‘meaning space’ is populated by either expressions related to ‘concrete’ properties or by ‘expressions pointing forward’ to other expressions and these ‘pointing-forward’ expressions are here called ‘abstract meaning’. While concrete meanings are usually ‘decidable’ in the everyday world situations as being ‘given’ (being ‘true’) or as ‘not being given’ (‘being false’), abstract meanings are as expressions ‘undefined’: they can lead to some concrete property which in turn perhaps can be decided or not.

The availability of ‘abstract expressions’ in ordinary language can be seen as a ‘problem’ or as a ‘blessing’. Being able to generate and use abstract terms manifests a great flexibility in talking — and thinking! — about possible realities which allow to overcome the dictatorship of the ‘now’ and the ‘individual single’. Without abstraction thinking would indeed be impossible. Thus if one understands that ‘thinking’ is a real process with sequences of different states which reveal eventually more abstract classes, structures, and changes, then abstraction is the ‘opener’ for more reality, the ‘enabler’ for a more broader and flexible knowledge. Only by ‘transcending’ the eternal ‘Now’ we get an access to phenomena like time, changes, all kinds of dynamics, and only thereby are ‘pictures of some possible future’ feasible!

Clearly, the potential of abstraction can also be a source of ‘non-real’ ideas, of ‘fantastic’ pictures, of ‘fake news’ and the like.

But these possible ‘failures’ — if they will be ‘recognized’ as failures! — are inevitable if one wants to dig out some ‘truth’ in the nearly infinite space of the unknown. Before the ‘knowledge that something is true’ one has to master a ‘path of trial and error’ consuming ‘time’ and ‘resources’.

This process of creating new abstract ideas to guide a search in the space of the unknown is the only key to find besides ‘errors’ sometimes some ‘truth’.

Thus the ‘problem’ with abstract ideas is an unavoidable condition to find necessary ‘truths’. Stepping back in the face of possible problems is no option to survive in the unknown future.

the formal view of the world according to bourbaki

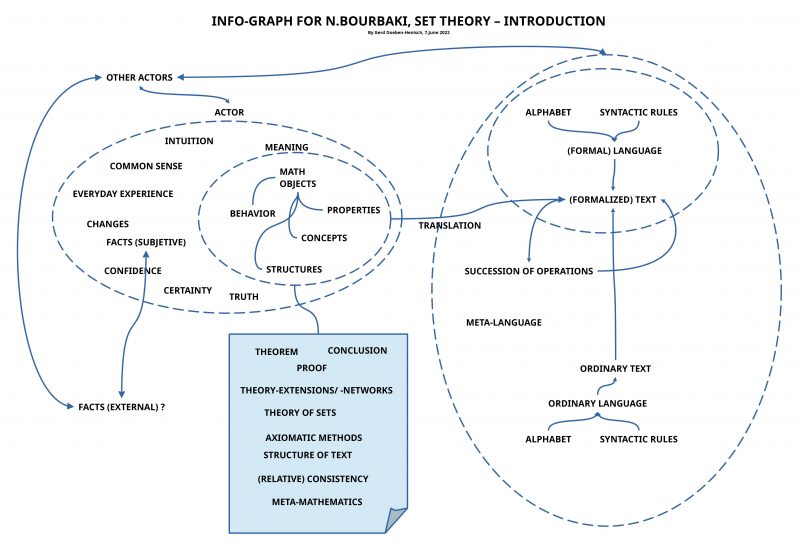
Language, object language, meta language

Talking about mathematical objects with their properties within an ordinary language is not simple because the expressions of an ordinary language are as such usually part of a network of meanings, which can overlap, which can be fuzzy, which are giving space for many interpretations. Additionally, that which is called a ‘mathematical object’ is not a kind of an object wich is given in the everyday world experience. What can be done in such a situation?

Bourbaki proposes to introduce a ‘specialized language’ constructed out of a finite set of elements constituting the ‘alphabet’ of a new language, together with ‘syntactical rules’, which describe how to construct with the elements of the alphabet chains of elements called ‘(well formed) expressions’, which constitute the ‘language’ L_O, which shall be used to talk about mathematical objects.

But because mathematics is not restricted to ‘static objects’ but deals also with ‘transformations’ (‘changes’) of objects, one needs ‘successions of objects’ (‘sequences’), which are related by ‘operations with mathematical objects’. In this case the operations are also represented by ‘expressions’ but these expressions are expressions of a ‘higher order’ which have as referenced subject those expressions which are representing objects . Thus, Bourbaki needs right from the beginning two languages: an ‘object language’ (expressions of a language L_O representing mathematical objects) and a ‘meta language’ LL (expressions referring to expressions of the object language L_O including certain ‘types of changes’ occurring with the object language expressions). Thus a mathematical language L_m consists in the combination of an object language L_O with a meta language LL (L_m = (L_O,LL)).

And, what becomes clear by this procedure, to introduce such a kind of mathematical language L_m one needs another language talking about the mathematical language L_m, and this is either the everyday (normal) language L, which is assumed to be a language which everybody can ‘understand’ and ‘apply correctly’, or it is a third specialized language LLL, which can talk with special expressions about the mathematical language L_m. Independent of the decision which solution one prefers, finally the ordinary language L will become the meta language for all other thinkable meta languages.

Translating(?) math objects into formal expressions

If the formalized expressions of the mathematical language (L_m = (L_O,LL)) would be the mathematical objects themselves, then mathematics would consist only of those expressions. And, because there would be no other criteria available, whatever expressions one would introduce, every expression would claim to be a relevant mathematical expression. This situation would be a ‘maximum of non-sense’ construct: nothing could be ‘false’.

Thus, the introduction of formal expressions of some language alone seems to be not enough to establish a language which is called a ‘mathematical’ language L_m different from other languages which talk about other kinds of objects. But what could it be which relates to ‘specific math objects’ which are not yet the expressions used to ‘refer’ to these specific math objects?

Everybody knows that the main reason for to ‘speak’ (or ‘write’) about math specific objects are humans which are claiming to be ‘mathematicians’ and which are claiming to have some ‘knowledge’ about specific objects called ‘math objects’ which are the ‘content’ which they ‘translate’ into the expressions of a certain language call ‘mathematical language’.[5] Thus, if the ‘math objects’ are not the used expressions themselves then these ‘math objects’ have to be located ‘inside of these talking humans’. According to modern science one would specify this ‘inside’ as ‘brain’, which is connected in complex ways to a body which in turn is connected to the ‘outside world of the body’. Until today it is not possible to ‘observe’ directly math objects assumed to be in the brain of the body of someone which claims to be a mathematician. Thus one mathematician A can not decide what another mathematician B has ‘available in his brain’ at some point of time.

Bourbaki is using some formulations in his introduction which gives some ‘flavor’ of this ‘being not able to translate it into a formalized mathematical language’. Thus at one position in the text Bourbaki is recurring to the “common sense” of the mathematicians [6] or to the “reader’s intuition”. [7] Other phrases refer to the “modes of reasoning” which cannot be formalized [8], or simply to the “experience” on which “the opinion rests”. [9] Expressions like ‘common sense’, ‘intuition’, ‘modes of reasoning’, and ‘experience’ are difficult to interpret. All these expressions describe something ‘inside’ the brains which cannot be observed directly. Thus, how can mathematician A know what mathematician B ‘means’ if he is uttering some statement or writes it down? Does it make a difference whether a mathematician is a man or a woman or is belonging to some other kind of a ‘gender’? Does it make a difference which ‘age’ the mathematician has? How ‘big’ he is? Which ‘weight’ he has?

Thus, from a philosophical point of view the question to the specific criteria which classify a language as a ‘mathematical language’ and not some other language leads us into a completely unsatisfying situation: there are no ‘hard facts’ which can give us a hint what ‘mathematical objects’ could be. What did we ‘overlook’ here? What is the key to the specific mathematical objects which inspired the brains of many many thousand people through centuries and centuries? Is mathematics a ‘big fake’ or is there more than this?

A mathematician as an ‘actor’?

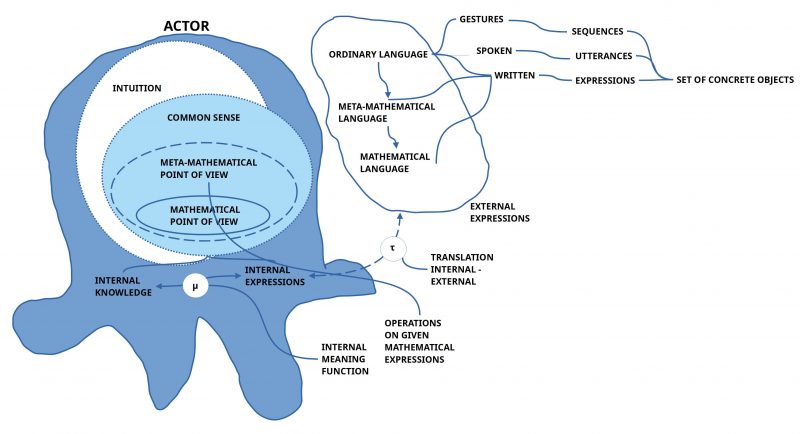
This last question “Is mathematics a ‘big fake’ or is there more than this?” can lead o the assumption, that it is not enough to talk about ‘mathematics’ by not including the mathematician itself. Only the mathematician is that ‘mysterious source’ of knowledge, which seems to trigger the production of ‘mathematical expressions’ in speaking or writing (or drawing). Thus a meta-mathematical — and thereby philosophical’ — ‘description’ of mathematics should have at least the ‘components’ (MA, L_O,LL,L) with ‘MA’ as abbreviation for the set of actors where each element of the set MA is a mathematician, and — this is decisive ! — it is this math actor MA which is in possession of those ‘criteria’ which decide whether an expression E belongs the ‘mathematical language L_m‘ or not.

The phrase of the ‘mathematician’ as a ‘mysterious source of knowledge’ is justified by an ’empirical observational point of view’: nobody can directly look into the brain of a mathematician. Thus the question of what an expression called ‘mathematical expression’ can ‘mean’ is in such an empirical view not decidable and appears to be a ‘mystery’.

But in the reality of everyday life we can observe, that every human actor — not only mathematicians — seems to be able to use expressions of the everyday language with referring to ‘internal states’ of the brain in a way which seems to ‘work’. If we are talking about ‘pain with my teeth’ or about ‘being hungry or thirsty’ or ‘having an idea’ etc. then usually other human actors seem to ‘understand’ what one is uttering. The ‘evidence’ of a ‘working understanding’ is growing up by the ‘confirmation of expectations’: if oneself is hungry, then one has a certain kind of ‘feeling’ and usually this feeling leads — depending from the cultural patterns one is living in — to a certain kind of ‘behavior’, which has — usually — the ‘felt effect’ of being again ‘not hungry’. This functional relation of ‘feeling to be hungry’, ‘behavior of consuming something’, ‘feeling of being not hungry again’ is an association between ‘bodily functions’ common to all human actors and additionally it is a certain kind of observable behavior, which is common to all human actors too. And it seems to work that human actors are able to associate ‘common internal states’ with ‘common observable behavior’ and associate this observable behavior with the ‘presupposed internal states’ with certain kinds of ‘expressions’. Thus although the internal states are directly not observable, they can become ‘communicated by expressions’ because these internal states are — usually — ‘common to the internal experience of every human actor’.

From this follows the ‘assumption’ that we should extend the necessary elements for ‘inter-actor communication’ with the factor of ‘common human actor HA experience’ abbreviated as ‘HA_X‘ (HA, HAX, MA, L_O,LL,L), which is usually accompanied by certain kinds of observable behavior ‘B_X‘, which can be used as point of reference for certain expressions ‘L_X‘, which ‘point to’ the associated intern al states HA_X, which are not directly observable. This yields the structure (HA, HA_X, MA, B_X, L_O,LL,L_X,L).

Having reached this state of assumptions, there arises an other assumption regarding the relationship between ‘expressions of a language’ — like (L_O,LL,L_X,L) — and those properties which are constituting the ‘meaning’ of these expressions. In this context ‘meaning’ is not a kind of an ‘object’ but a ‘relation’ between two different things, the expressions at one side and the properties ‘referred to’ on the other side. Moreover this ‘meaning relation’ seems not to be a ‘static’ relation but a ‘dynamic’ one, associating two different kinds of properties one to another. This reminds to that what mathematicians call a ‘mapping, a function’, and the engineers a ‘process, an operation’. If we abbreviate this ‘dynamic meaning relation’ with the sign ‘μ’, then we could agree to the convention ‘μ_X : L_X <—> (B_X,HA_X)’ saying that there exists a meaning function μ_X which maps the special expressions of L_X to the special internal experience HA_X, which in turn is associated with the special behavior B_X. Thus, we extend our hypothetical structure to the format (HA, HA_X, MA, B_X, L_O,LL,L_X,L,μ_X).

With these assumptions we are getting a first idea how human actors in general can communicate about internal, directly not observable states, with other human actors by using external language expressions. We have to notice that the assumed dynamic meaning relation μ_X itself has to be located ‘inside’ the body, inside’ the brain. This triggers the further assumption to have ‘internal counterparts’ of the external observable behavior as well as external expressions. From this follows the further assumption that there must exists some ‘translation/ transformation’ ‘τ’ which ‘maps’ the internal ‘counterparts’ of the observable behavior and the observable expressions into the external behavior.(cf. figure 2) Thus, we are reaching the further extended format: (HA, HA_X, MA, B_X, L_O,LL,L_X,L,μ_X,τ).

Mathematical objects

Accepting the basic assumptions about an internal meaning function μ_X as well an internal translation function τ narrows the space of possible answers about the nature of ‘math objects’ a little bit, but as such this is possibly not yet a satisfying answer. Or, have we nevertheless yet to assume that ‘math objects’ and related ‘modes of reasoning’ are also rooted in internal properties and dynamics of the brain which are ‘common to all humans’?

If one sees that every aspect of the human world view is encoded in some internal states of the brain, and that what we call ‘world’ is only given as a constructed virtual structure in the brains of bodies including all the different kinds of ‘memories’, then there is no real alternative to the assumption that ‘math objects’ and related ‘modes of reasoning’ have to be located in these — yet not completely decoded — inner structures and dynamics of the brain.

From the everyday experience — additionally enlightened by different scientific disciplines, e.g. experimental (neuro) psychology — we know that the brain is — completely automatic — producing all kinds of ‘abstractions’ from concrete ‘perceptions’, can produce any kinds of ‘abstractions of abstractions’, can ‘associate’ abstractions with other abstractions, can arrange many different kinds of memories to ‘arrangements’ representing ‘states’/ ‘situations’, ‘transformations of states’, ‘sequences of states’ and the like. Thus everything which a ‘mathematical reasoning’ HA_m needs seems to be available as concrete brain state or brain activity, and this is not only ‘special’ for an individual person alone, it is the common structure of all brains.

Therefore one has to assume that the set of mathematicians MA is a ‘subset’ of the set of human actors HA in general. From this one can further assume that the ‘mathematical reasoning’ HA_m is a subset of the general human everyday experience HA_X. And, saying this, the meaning function μ_X as well as the translation function τ should be applicable also to the mathematical reasoning and the mathematical objects as well: (HA, MA, HA_X, HA_m, B_X, L_O,LL,L_X,L,μ_X,τ).

These assumptions would explain why it is not only possible but ‘inevitable’ to use the everyday language L to introduce and to use a mathematical language L_m with different kinds of sub-languages (L_O,LL, LLL, …). Thus in analogy to the ‘feeling’ ‘to be hungry’ with a cultural encoded kind of accompanying behavior B_X we have to assume that the different kinds of internal states and transformations in the case of mathematical reasoning can be associated with an observable kind of ‘behavior’ by using ‘expressions’ embedded (encoded) in certain kinds of ‘behavior’ accepted as ‘typical mathematical’. Introducing expressions like ‘0’, ‘1’, ‘2’, …, ’10’, … (belonging to a language L_o) for certain kinds of ‘objects’ and expressions like ‘+’, ‘-‘ … for certain kinds of operations with these before introduced objects (belonging to a language LL) one can construct combined expressions like ‘1+2=3’ (belonging to a mathematical language L_m). To introduce ‘more abstract objects’ like ‘sets’, ‘relations’, ‘functions’ etc. which have no direct counterpart in the everyday world does not break the assumptions. The everyday language L operates already only with abstract objects like ‘cup’, ‘dog’, ‘house’ etc. The expression ‘cup’ is an abstract concept, which can easily be associated with any kind of concrete phenomena provided by perceptions introducing ‘sets of different properties’, which allow the construction of ‘subsets of properties’ constituting a kind of ‘signature’ for a certain abstract ‘class’ which only exists in the dynamics of the brain. Thus having a set C named ‘cup’ introduces ‘possible elements’, whose ‘interpretation’ can be realized by associating different kinds of sets of properties provided by ‘sensory perception’. But the ‘memory’ as well as the ‘thinking’ can also provide other kinds of properties which can be used too to construct other ‘classes’.

In this outlined perspective of brain dynamics mathematics appears to be a science which is using these brain dynamics in a most direct way without to recur to the the huge amount of everyday experiences. Thus, mathematical languages (today summarized in that language, which enables the so called ‘set theory’) and mathematical thinking in general seems to reflect the basic machinery of the brain processing directly across all different cultures. Engineers worldwide speaking hundreds of different ‘everyday languages’ can work together by using mathematics as their ‘common language’ because this is their ‘common thinking’ underlying all those different everyday languages.

Being a human means being able to think mathematically … besides many other things which characterizes a human actor.

Epiloge

Basically every ordinary language offers all elements which are necessary for mathematics (mathematics is the kernel of every language). But history illustrates that it can be helpful to ‘extend’ an ordinary language with additional expressions (L_o, LL, LLL, …). But the development of modern mathematics and especially computer science shows increasing difficulties by ‘cutting away’ everyday experience in case of elaborating structures, models, theories in a purely formal manner, and to use these formal structures afterwards to interpret the everyday world. This separates the formal productions from the main part of users, of citizens, leading into a situation where only a few specialist have some ‘understanding’ (usually only partially because the formalization goes beyond the individual capacity of understanding), but all others have no more an understanding at all. This has he flavor of a ‘cultural self-destruction’.

In the mentioned oksimo software as part of a new paradigm of a more advanced citizen science this problem of ‘cultural self-destruction’ is avoided because in the format of a ‘computer aided sustainable applied empirical theory (CSAET) the basic language for investigating possible futures is the ordinary language which can be extend as needed with quantifying properties. The computer is not any more needed for ‘understanding’ but only for ‘supporting’ the ‘usage’ of everyday language expressions. This enables the best of both worlds: human thinking as well as machine operations.

COMMENTS

Def: wkp := Wikipedia; en := English

[1a] Bourbaki Group, see: https://en.wikipedia.org/wiki/Nicolas_Bourbaki

[1b] Theory of Sets with a chapter about structures, see: https://en.wikipedia.org/wiki/%C3%89l%C3%A9ments_de_math%C3%A9matique

[2] Gerd Doeben-Henisch, “Extended Concept for Meaning Based Inferences, Version 1”, August 2020, see: https://www.uffmm.org/wp-content/uploads/2020/08/TruthTheoryExtended-v1.pdf

[3] Gerd Doeben-Henisch, “From SYSTEMS Engineering to THEORY Engineering”, June 2022, see: https://www.uffmm.org/2022/05/26/from-systems-engineering-to-theory-engineering/

[4] Humans, How many years ago?, see: wkp (en): https://en.wikipedia.org/wiki/Human#:~:text=Homo%20sapiens,-Linnaeus%2C%201758&text=Anatomically%20modern%20humans%20emerged%20around,local%20populations%20of%20archaic%20humans.

[5] The difference between ‘talking’ about math objects and ‘writing’ is usually not thematised in the philosophy of mathematics. Because the ordinary language is the most general ‘meta language’ for all kinds of specialized languages and the primary source of the ordinary language then ‘speaking’ is perhaps not really a ‘trivial’ aspect in understanding the ‘meaning’ of any kind of language.

[6] “But formalized mathematics cannot in practice be written down in full, and therefore we must have confidence in what might be called the common sense of the mathematician …”. (p.11)

[7] “Sometimes we shall use ordinary language more loosely … and by indications which cannot be translated into formalized language and which are designed to help the reader to reconstruct the whole text. Other passages, equally untranslatable into formalized language, are introduced in order to clarify the ideas involved, if necessary by appealing to the reader’s intuition …”(p.11)

[8] “It may happen at some future date that mathematicians will agree to use modes of reasoning which cannot be formalized in the language described here : it would then be necessary, if not to change the language completely, at least to enlarge its rules of syntax.”(p.9)

[9] “To sum up, we believe that mathematics is destined to survive … but we cannot pretend that this opinion rests on anything more than experience.”(p.13)