eJournal: uffmm.org
ISSN 2567-6458, 22.Sept – 24.Sept 2021
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de
(Some minor corrections: 23.Sept 2021)
(A substantial extension: 24.Sept.2021)
CONTEXT
This text is part of a philosophy of science analysis of the case of the oksimo software (oksimo.com). A specification of the oksimo software from an engineering point of view can be found in four consecutive posts dedicated to the HMI-Analysis for this software.[*]
THE BOOK: THEORY OF SETS
Covered under the pseudonym of N.Bourbaki [1] appeared 1970 the French edition of a book which 1968 already had been translated into English (reprinted 1970) called Theory of Sets.[2] This book is the first book of a series about ELEMENTS OF MATHEMATICS.
To classify this book about set theory as a book of Metamathematics and as such as a book in the perspective of Philosophy of Science will become clear if one starts reading the book.[3]
MATHEMATICS WITH ONE LANGUAGE
It is the basic conviction of the Bourbaki book, that “… it is known to be possible … to derive practically the whole of known mathematics from a single source the Theory of Sets.” (p.9) And from this Bourbaki concludes, that it will be sufficient “… to describe the principles of a single formalized language, to indicate how the Thory of Sets could be written in this language, and then to show how the various branches of mathematics … fit into this framework.”(p.9)
Thus, the content of mathematics — whatever it is — can according to Bourbaki be described in one single language [Lm] and the content will be called Theory of Sets [T] .
METAMATHEMATICS
Because the one single language Lm used to describe the Theory of Sets shall be a language with certain properties one has to define these properties with some other language, which is talking about Lm. As language for this job Bourbaki is using the ordinary language [Lo].(p.9) But the reasoning within which one is using this ordinary language is called metamathematics (cf. P.10f). Within the metamathematical point of view the language Lm under investigation is seen as a set of previously given objetcs without any kind of meaning, where only the assigned order is of importance.(cf. p.10): “… metamathematical ‘arguments’ usually assert that when a succession of operations has been performed on a text of a given type, then the final text will be of another given type.”(p.10)
What looks here at first glance as the complete formalization of mathematics it is not. Bourbaki states clearly that “formalized mathematics cannot in practice be written down in full“(p.11) There has to be assumed as ‘last resort’ the assumption of a common sense of the mathematician and the intuition of the reader. (cf. p.11)
COGNITIVE-SEMIOTIC TURN
This conflict between at one hand of the idea of a formalization of Mathematics by a formalized language Lm and on the other hand by the well known proof of Gödel [4] of the incompleteness of the axioms for classical arithmetic (cf. p.12) is not a real conflict as long as one takes into account — as Bourbaki points out — that the ‘content of mathematics’ is only given in different layers of languages (Lm, Lo, …) which again are embedded in a presupposed ‘common sense’ which is nothing else as the cognitive machinery of human persons including an embedded meaning function relating different kinds of knowledge into different kinds of — internal as well as external — expressions of some language L. Thus any kind of a ‘reduction of meaning’ seems never to be a ‘complete reduction’ but only a ‘technical reduction’ to introduce some ‘artificial (abstract) objetcs’ which can only work because of their embedding in some richer context.
This new perspective can be called the cognitive-semiotic turn which became possible by new insights of modern brain sciences in connection with pysychology and semiotics.
From this new point of view one can derive the idea of embedding metamathemics in a more advanced actor theory providing all the ingredients to make metamathematics more ‘rational’.
OUTLINE OF ACTOR THEORY
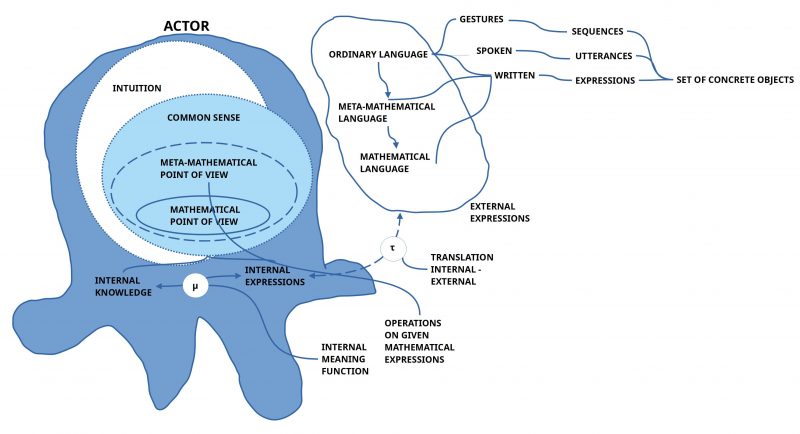
The details of the Actor Theory [AT] can become quite complex. Here a first outline of the basic ideas and what this can mean for a metamathematical point of view of mathematics.
World is not World
The main idea is founded in the new insights of Biology and Neuro-Psychology of the handling of body-world interactions as exercised by humans. One of the main insights is rooted back to von Uexküll [5] more than 100 years ago, when he described how every biological organism perceives and handles some world outside of the body with the inner neuronal structures given! Thus different life forms in the same outside world W will peceive and act neuronally in different worlds! Brain X acts in world X which is somehow related to the outside world W as well as Brain Y acts in world Y which also is somehow related to the outside world W.
These basic insights relate as well to more developed life forms as such as humans are. We as humans do not perceive and think the world W outside of our bodies ‘as it is’ but only as our brain inside our body can process all the body states related to the outside world in the mode of the inside brain. Thus if the different human individuals would have different brains they would live in different worlds and their would be no chance of a simple communication. But as we know from physiological and behavioral studies humans can to some extend communicate successfully. Thus there exists inside of every human individual a human-processed world h(W) which is different from other life-forms like a rat, a worm, an octopus, etc.
From this basic insight it follows that if we speak about the world W we do indeed not speak about the world W directly but about the world W as it is processed in a human-specific manner, the world h(W). This has many implications.
- Because we know already that the world h(W) is not a static but a dynamic world depending from our learning history it can happen — and it happens all the time — that different individuals have different learning histories. This can result in quite strong differences of experience and knowledge attached to different individuals, which can prevent a simple understanding between such individuals: the learned world h1(W) can to some degree be different from the learned world h2(W) such that a simple and direct understanding will not be possible.
- This difference between the outside world W and the processed inside world h(W) relates to the communication too! The spoken or written expressions E of some language L are belonging to the outside world. They have a counterpart in the inner world as inner expressions E*, which can be associated with all kinds of processed inner states of the inner world h(W) = W*. These possible — and learned — associations between inner expressions and inner states belonging to h(W) is assumed here to be that what commonly is called meaning. Thus one has to assume an internal meaning function μ which maps the internal expressions E* of some internal language L* into parts of the internally processed world h(W)=W* and vice versa. Thus we have μ: E* <—> W*. Thus μ(e*) would point to some part w* of the internally processed world W* as the ‘meaning’ of the internal expression e*.
- This semiotic architecture of human beings enables a nearly infinite space of expressions as well as associated meanings definable during learning processes. This is powerful, but it is also very demanding for the speaker-hearer: to enable a succesful communication between different speaker-hearer these have to train their language usage under sufficient similar conditions thereby constructing individual meaning functions which work — hopefully — sufficiently similar. If not then communication can slow down, can produce lots of misunderstandings or can even break down completely. [6]
- In the case of mathematics it is a long debated question whether mathematics can be reduced to the expressions Em of some mathematical language Lm or if mathematics has some mathematical objects on its own which are different from the expressions. If one would assume that mathematics has no objects on its own but only some expressions Em, then it would become difficult to argue whether exactly these expressions Em should be used and not some other expressions Ex. Moreover to classify expressions as ‘axioms’ or ‘theorems’ would be completely arbitrary. The only ‘anchor’ of non-arbitrariness would consist in some formal criteria of a formal consistency which would disable the formal generation of pairs of expressions {a,a*} where one is excluding the other. But even such a formal consistency presupposes some criteria which are beyond the expressions as such! Thus mathematics would need some criteria outside mathematics. This can be understood as an argument for metamathematics. But according to Bourbaki metamathematics is defined as a set of operations on given expressions without a specific meaning. This is not enough to establish formal consistency! Thus even metamathematics is pointing to something outside of given mathematical expressions. What can this be?
PART 2
To be continued …
COMMENTS
[*] More recent versions of the specification of the oksimo oftware can be found in the bolg oksimo.org. Unfortunately are the texts in that blog — at the time if this writing — still only in German. Hopefully this will change in the future.
[1] Bourbaki group in Wikipedia [EN]: https://en.wikipedia.org/wiki/Nicolas_Bourbaki
[2] N.Bourbaki (1970), Theory of Sets, Series: ELEMENTS OF MATHEMATICS, Springer, Berlin — Heidelberg — New York (Engl. Translation from the French edition 1970)
[3] The first time when the author of this text has encountered the book was some time between 1984 – 1987 while being a PhD-student at the Ludwig-Maximilians Univesty [LMU] in Munich. It was in a seminar with Prof. Peter Hinst about structural approaches to Philosophy of Science. The point of view at that time was completely different to the point of view applied in this text.
[4] Kurt Goedel. Über formal unentscheidbare Sätze der Principia
Mathematica und verwandter Systeme, i. Monatshefte fuer
Mathematik und Physik, 38:173–98, 1931.
[5] Jakob von Uexküll, 1909, Umwelt und Innenwelt der Tiere. Berlin: J.Springer.
[6] Probably everybody has made the experience in his life of being part of a situation where nobody speaks a language, which one is used to speak …
