Journal: uffmm.org,
ISSN 2567-6458, July 9, 2019
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de

CONTEXT

This is the next step in the python3 programming project. The first step can be found here. The overall context is still the python Co-Learning project.

PROGRAMMING TOOLS

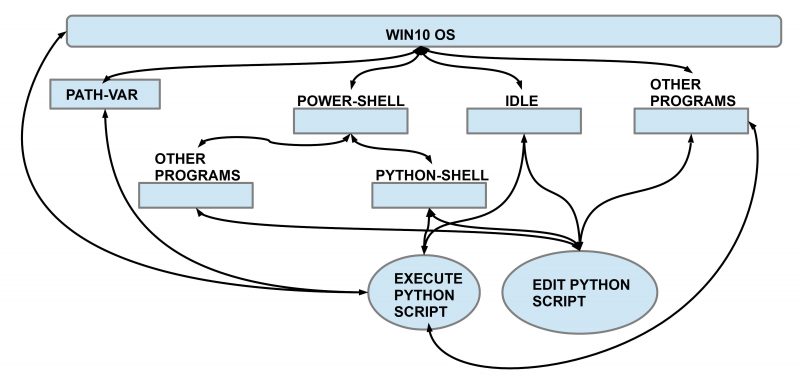
In this second session we extend the overview of the possible programming tools, how they are interrelated, and how they work.

In the figure above you can see the windows 10 operating system as the root system for everything else. The win10 system communicates with the PATH-variable and uses this information for many operations. How on can edit this variable has been shown in the last session.

One can activate directly from the win10 system the power-shell with a command-line interface. Entering the right code one can activate from the power-shell either directly a python-shell for python commands or one can activate other programs like the editor ‘notepad’ or ‘notepad++’. With such editors one can edit python scripts, store them, and then run these scripts from the power-shell by calling a python-shell with these scripts as arguments (as shown in the first session).

The python shell allows the direct entering of python commands and gives immediately feedback whether it works and how. Therefore one calls this an interactive shell which is very handy to check quickly some commands and their effects.

Another tool, which we will use in this session, is the integrated script environment (IDLE). This is like the python-shell but with some additional functionalities (see below). The main usage is for editing larger python scripts with a built-in editor and for running these scripts.

THE IDLE TOOL

To use this new tool you can press the windows button to see the list of all apps (programs) available on your computer. Under ‘P’ you will find python 3.7.3 and within python you will find an entry for IDLE. By selecting this item and clicking on the right mouse-button you can select the option to attach this icon to the task bar. If it is there you can use it.

If you start the IDLE tool by clicking on the icon from the task bar it opens as a new python interactive shell with some more options.

A first thing you can do is to ask for the actual path you are in. For this you have to import the python module ‘os’ (operating system) and use the command ‘getcwd()‘ from this module. Entering ‘os.getcwd()‘ in the python command line generates the actual path as output on the next line.

>>> import os
>>> os.getcwd()
‘C:\\Users\\gerd_2\\AppData\\Local\\Programs\\Python\\Python37-32’
>>>

This reveals that the actual path is pointing to the location of the python exe module (on my pc). This is not what I want because I have created in the first session a folder with name ‘code’ in my home directory ‘\Users\gerd_2’. From inside of the IDLE tool it is not possible to change the actual path.  But python as language provides lots of options to do this. One option is described below:

The module os offers several functions. Besides the function ‘os.getcwd()’ which we have used already there is another command ‘os.chdir(pathname)‘. But to directly change the actual path one has to be cautious because the path ‘C:\\Users\gerd_2\code‘ includes the ‘\’-sign, this cannot be read directly by the os.chdir() command. You can surround this problem by using the ‘\’-sign twice: first as an ‘escape sign’ and then as the ‘object sign’, resulting in the following command format: ‘C:\\Users\\gerd_2\\code‘. Entering this nothing is given as a result, and when you repeat the question ‘os.getcwd()’ you will receive as new answer the new path. Here the dialog with the python-shell:

Python 3.7.3 (v3.7.3:ef4ec6ed12, Mar 25 2019, 21:26:53) [MSC v.1916 32 bit (Intel)] on win32

Type “help”, “copyright”, “credits” or “license()” for more information.

>>> import os

>>> os.getcwd()

‘C:\\Users\\gerd_2\\AppData\\Local\\Programs\\Python\\Python37-32’

>>> os.chdir(‘C:\\Users\\gerd_2\\code’)

>>> os.getcwd()

‘C:\\Users\\gerd_2\\code’

>>>

You can see that the python command ‘os.getcwd() has been used twice. If you want to repeat some command you can call-back the command history of the python-shell with the keystrokes ‘ALT+P‘. This recalls the past (P) of the command history.

Comment: In the command

>> os.chdir(‘C:\\Users\\gerd_2\\code’)

I have used the back-slash sign ‘\’ twice to make the string fit as argument for the ‘os.chdir()’ command. As one can learn does python allow another solution, which looks like this:

>> os.chdir(r’C:\Users\gerd_2\code’)

The solution is to use an additional ‘r’ directly before the string ‘…’ telling the python interpreter that the following string has to be understood as a raw string. This works, try it out 🙂

IDLE AND EXECUTION OF A SCRIPT

Now if we are in the target folder for my scripts we can look to all files which are in this folder actually. For this we can use the python command ‘os.listdir()’:

>>> os.listdir()

[‘savesrc.txt’, ‘script1.py’, ‘script1.pyw’, ‘script1b.py’, ‘showargs.py’, ‘threenames.py’, ‘tst1.py’, ‘what.py’, ‘what2.py’, ‘__pycache__’]

>>>

You can detect in this list the python script ‘scrpt1.py’. Entering the name of this script either with .py extension or without will not enable an execution:

>>> script1.py

Traceback (most recent call last):

File “<pyshell#6>”, line 1, in <module>

script1.py

NameError: name ‘script1’ is not defined

From the first session we know that we can start the script within the power-shell directly. For this we have to activate the powershell, have to go into the desired folder ‘code’ …

PS C:\Users\gerd_2> cd code

PS C:\Users\gerd_2\code> dir

Verzeichnis: C:\Users\gerd_2\code

Mode LastWriteTime Length Name

—- ————- —— —-

d—– 04.07.2019 19:03 __pycache__

-a—- 01.07.2019 18:44 182 savesrc.txt

-a—- 01.07.2019 18:41 92 script1.py

-a—- 24.06.2019 23:23 126 script1.pyw

-a—- 24.06.2019 22:43 128 script1b.py

-a—- 04.07.2019 18:51 56 showargs.py

-a—- 28.06.2019 00:29 162 threenames.py

-a—- 24.06.2019 21:16 120 tst1.py

-a—- 24.06.2019 22:49 126 what.py

-a—- 24.06.2019 23:56 136 what2.py

… and then we can start the python-script ‘script1.py’:

PS C:\Users\gerd_2\code> python script1.py

win32

1267650600228229401496703205376

pythonpythonpythonpythonpythonpythonpythonpython

PS C:\Users\gerd_2\code>

But because we will here use the IDLE tool we proceed differently. We open the File-Menue to get the desired file script1.py:

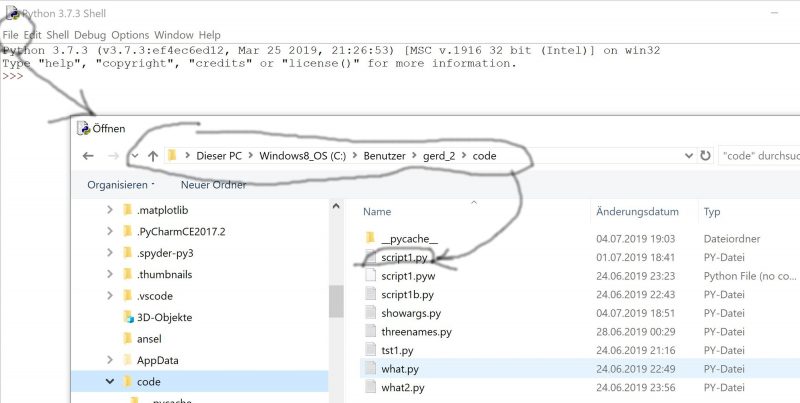
Then we load  the python-script script1.py in the editor of the IDLE tool:

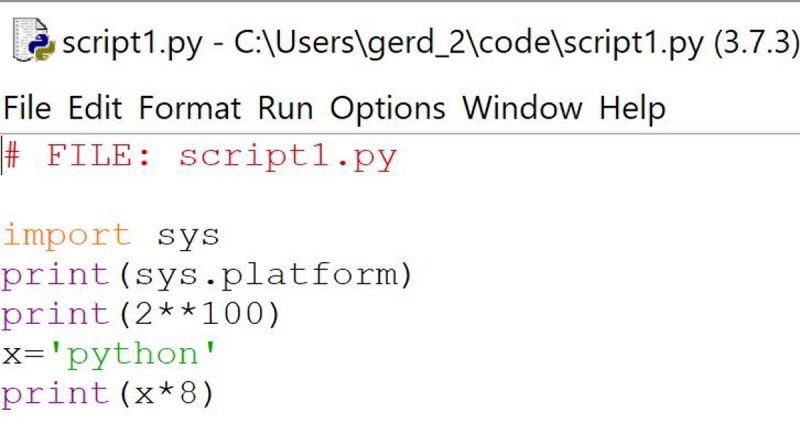
and then activate the RUN button for execution:

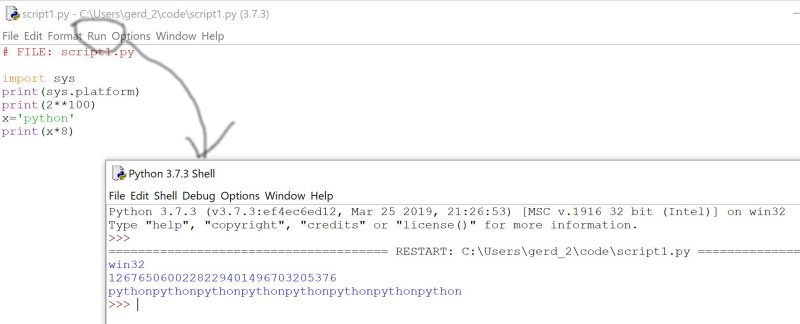
The script will then be executed and you will see the effect of the execution in the python shell. This looks the same as when you would have called the script within the power-shell calling  the python-shell.

There is still the other option to get the module running by the import command:

>>> import script1.py

win32

1267650600228229401496703205376

pythonpythonpythonpythonpythonpythonpythonpython

Traceback (most recent call last):

File “<pyshell#7>”, line 1, in <module>

import script1.py

ModuleNotFoundError: No module named ‘script1.py’; ‘script1’ is not a package

>>>

The import call works, but at the same time the python-shell states some error, that ‘script1.py’ is not recognized as a true module. This has to be clarified in the next session.

One possible continuation can be found HERE.