eJournal: uffmm.org
ISSN 2567-6458, 07.March 22 – 12.March 2022, 10:55h
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de
BLOG-CONTEXT
This post is part of the Philosophy of Science theme which is part of the uffmm blog.
PREFACE
In this post a short summary of Poppers view of an empirical theory is outlined as he describes it in his article “Conjectural Knowledge: My Solution of the Problem of Induction” from 1971.[1] The view of Popper will be commented and the relationsship to the oksimo paradigm of the author will be outlined.
Empirical Theory according to Popper in a Nutshell
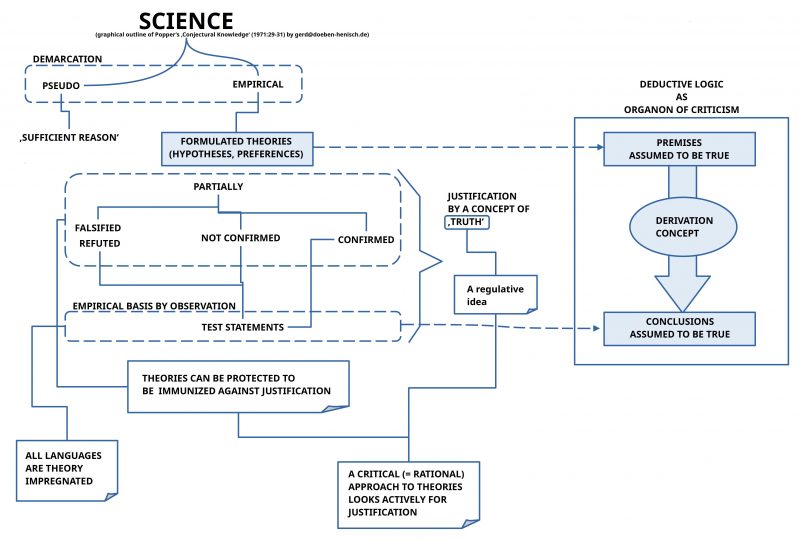
POPPER’S POSITION 1971
In this article from 1971 Popper discusses several positions. Finally he offers the following ‘demarcation’ between only two cases: ‘Pseudo Science’ and ‘Empirical Science’.(See p.29) In doing so this triggers the question how it is possible to declare something as an ‘objective empirical theory’ without claiming to have some ‘absolute truth’?
Although Popper denies to have some kind of absolute truth he will “not give up the search for truth”, which finally leads to a “true explanatory theory”.(cf. p.29) “Truth” plays the “role of a regulative idea”.(cf. p.30) Thus according to Popper one can “guess for truth” and some of the hypotheses “may well be true”.(cf.p.30)
In Popper’s view finally ‘observation’ shows up as that behaviour which enables the production of ‘statements’ as the ’empirical basis’ for all arguments.(cf.p.30) Empirical statements are a ‘function of the used language’.(cf. p.31)
This dimension of language leads Popper to the concept of ‘deductive logic’ which describes formal mechanisms to derive from a set of statements — which are assumed to be true — those statements, which are ‘true’ by logical deduction only. If statements are ‘logically false’ then this can be used to classify the set of assumed statements as ‘logically not consistent’. (cf. p.31)
comments on popper’s 1971-position 50 years later
The preceding outline of Popper’s position reveals a minimalist account of the ingredients of an ‘objective empirical theory’. But we as the readers of these ideas are living 50 years later. Our minds are shaped differently. The author of this text thinks that Popper is basically ‘true’, although there are some points in Popper’s argument, which deserve some comments.
Subjective – Absolute
Popper is moving between two boundaries: One boundary is the so called ‘subjective believe’ which can support any idea, and which thereby can include pure nonsense; the other boundary is ‘absolute truth’, which is requiring to hold all the time at all places although the ‘known world’ is evidently showing a steady change.
Empirical Basis
In searching for a possible position between these boundaries, which would allow a minimum of ‘rationality’, he is looking for an ’empirical Basis’ as a point of reference for a ‘rational theory’. He is locating such an empirical basis in ‘observation statements’ which can be used for ‘testing a theory’.
In his view a ‘rational empirical theory’ has to have a ‘set of statements’ (often called ‘assumptions’ of the theory or ‘axioms’) which are assumed to ‘describe the observable world’ in a way that these statements should be able to be ‘confirmed’ or be ‘falsified’.
Confirmation – Falsification
A ‘confirmation’ does not imply that the confirmed statement is ‘absolutely true’ (his basic conviction); but one can experience that a confirmed statement can function as a ‘hypothesis/ conjecture’ which ‘workes in the actual observation’. This does not exclude that it perhaps will not work in a future test. The pragmatical difference between ‘interesting conjectures’ and those which are of less interest is that a ‘repeated confirmation’ increases the ‘probability’, that such a confirmation can happen again. An ‘increasing probability’ can induce an ‘increased expectation’. Nevertheless, increased probabilities and associated increased expectations are no substitutes for ‘truth’.
A test which shows ‘no confirmation’ for a logically derived statement from the theory is difficult to interpret:
Case (i): A theory is claiming that a statement S refers to a proposition A to be ‘true in a certain experiment’, but in the real experiment the observation reveals a proposition B which translates to non-A which can interpreted as ‘the opposite to A is being the case’ (= being ‘true’). This outcome will be interpreted in the way that the proposition B interpreted as ‘non-A’ contradicts ‘A’ and this will be interpreted further in the way, that the statement S of the theory represents a partial contradiction to the observable world.
Case (ii): A theory is claiming that a statement S refers to a proposition A to be ‘true in a certain experiment’, but in the real experiment the observation reveals a proposition B ‘being the case’ (= being ‘true’) which shows a different proposition. And this outcome cannot be related to the proposition ‘A’ which is forecasted by the theory. If the statement ‘can not be interpreted sufficiently well’ then the situation is neither ‘true’ nor ‘false’; it is ‘undefined’.
Discussion: Case (ii) reveals that there exist an observable (empirical) fact which is not related to a certain ‘logically derived’ statement with proposition A. There can be many circumstances why the observation did not generate the ‘expected proposition A’. If one would assume that the observation is related to an ‘agreed process of generating an outcome M’, which can be ‘repeated at will’ from ‘everybody’, then the observed fact of a ‘proposition B distinguished from proposition A’ could be interpreted in the way, that the expectation of the theory cannot be reproduced with the agreed procedure M. This lets the question open, whether there could eventually exist another procedure M’ producing an outcome ‘A’. This case is for the actors which are running the procedure M with regard to the logically derived statement S talking about proposition A ‘unclear’, ‘not defined’, a ‘non-confirmation’. Otherwise it is at the same time no confirmation either.
Discussion: Case (i) seems — at a first glance — to be more ‘clear’ in its interpretation. Assuming here too that the observation is associated with an agreed procedure M producing the proposition B which can be interpreted as non-A (B = non-A). If everybody accepts this ‘classification’ of B as ‘non-A’, then by ‘purely logical reasons’ (depending from the assumed concept of logic !) ‘non-A’ contradicts ‘A’. But in the ‘real world’ with ‘real observations’ things are usually not as ‘clear-cut’ as a theory may assume. The observable outcome B of an agreed procedure M can show a broad spectrum of ‘similarities’ with proposition A varying between 100% and less. Even if one repeats the agreed procedure M several times it can show a ‘sequence of propositions <B1, B2, …, Bn>’ which all are not exactly 100% similar to proposition A. To speak in such a case (the normal case!), of a logical contradiction it is difficult if not impossible. The idea of Popper-1971 with a possible ‘falsification’ of a theory would then become difficult to interpret. A possible remedy for this situation could be to modify a theory in the way that a theory does forecast only statements with a proposition A which is represented as a ‘field of possible instances A = <a1, a2, …, am>’, where every ‘ai‘ represents some kind of a variation. In that modified case it would be ‘more probable’ to judge a non-confirmation between A as <a1, a2, …, am> and B as <B1, B2, …, Bn>, if one would take into account the ‘variability’ of a proposition.[3]
Having discussed the case of ‘non-confirmation’ in the described modified way this leads back again to the case of ‘confirmation’: The ‘fuzziness’ of observable facts even in the context of agreed procedures M of observation, which are repeatable by everyone (usually called measurement) requires for a broader concept of ‘similarity’ between ‘derived propositions’ and ‘observed propositions’. This is since long a hot debated point in the philosophy of science (see e.g. [4]). Until now does no general accepted solution exist for this problem.
Thus the clear idea of Popper to associate a theory candidate with a minimum of rationality by relating the theory in an agreed way to empirical observations becomes in the ‘dust of reality’ a difficult case. It is interesting that the ‘late Popper’ (1988-1991) has modified his view onto this subject a little bit more into the direction of the interpretation of observable events (cf. [5])
Logic as an Organon
In the discussion of the possible confirmation or falsification of a theory Popper uses two different perspectives: (i) in a more broader sense he is talking about the ‘process of justification’ of the theoretical statements with regard to an empirical basis relying on the ‘regulative idea of truth’, and (ii) in a more specialized sense he is talking about ‘deductive logic as an organon of criticism’. These two perspectives demand for more clarification.
While the meaning of the concept ‘theory’ is rather vague (statements, which have to be confirmed or falsified with respect to observational statements), the concept ‘deductive logic as an organon’ isn’t really clearer.
Until today we have two big paradigms of logic: (i) the ‘classical logic’ inspired by Aristotle (with many variants) and (ii) ‘modern formal logic’ (cf. [6]) in combination with modern mathematics (cf. [7],[8]). Both paradigms represent a whole universe of different variants, whose combinations into concrete formal empirical theories shows more than one paradigm.(cf. [4], [8], [10])
As outlined in the figure above the principal idea of logic in general follows the following schema: one has a set of expressions of some language L for which one assumes at least, that these expressions are classified as ‘true expressions’. According to an agreed procedure of ‘derivation’ one can derive (deduce, infer, …) other expressions of the language which are assumed to be classified as ‘true’ if the assumptions hold.[11]
The important point here is, that the modern concept of logic does not explain, what ‘true’ means nor exists there an explanation, how exactly a procedure looks like which enables the classification of an expression as ‘being true’. Logic works with the minimalist assumption that the ‘user of logic’ is using statements which he assumes to be ‘true’ independent of how this classification came into being. This frees the user of logic to deal with the cumbersome process of clarifying the meaning and the existence of something which makes a statement ‘true’, but on the other side the user of modern logic has no real control whether his ‘concept of derivation’ makes any sense in a real world, from which observation statements are generated claiming to be ’empirically true’, and that the relationships between these observational statements are appropriately ‘represented’ by the formal derivation concept. Until today there exists no ‘meta-theory’ which explains the relationship between the derivation concept of formal logic (there are many such concepts!) and the ‘dynamics of real events’.
Thus, if Popper mentions formal logic as a tool for the handling of assumed true statements of a theory, it is not really clear whether such a formal logical derivation really is appropriate to explain the ‘relationships between assumed true statements’ without knowing, which kind of reality is ‘designated’/ ‘referred to’ by such statements and their relationships between each other.
(Formalized) Theory and Logic
In his paper Popper does not explain too much what he is concretely mean with a (formalized) theory. Today there exist many different proposals of formalized theories for the usage as ’empirical theories’, but there is no commonly agreed final ‘template’ of a ‘formal empirical theory’.
Nevertheless we need some minimal conception to be able to discuss some of the properties of a theory more concretely. I will address this problem in another post accompanied with concrete applications.
COMMENTS
[1] Karl R.Popper, Conjectural Knowledge: My Solution of the Problem of Induction, in: [2], pp.1-31
[2] Karl R.Popper, Objective Knowledge. An Evolutionary Approach, Oxford University Press, London, 1972 (reprint with corrections 1973)
[3] In our everyday use of our ‘normal’ language it is the ‘normal’ case that a statement S like ‘There s a cup on the table’ can be interpreted in many different ways depending which concrete thing (= proposition B of the above examples) called a ‘cup’ or called ‘table’ can be observed.
[4] F. Suppe, Ed., The Structure of Scientific Theories, University of
Illinois Press, Urbana, 2nd edition, 1979.
[5] Gerd Doeben-Henisch, 2022,(SPÄTER) POPPER – WISSENSCHAFT – PHILOSOPHIE – OKSIMO-DISKURSRAUM, in: eJournal: Philosophie Jetzt – Menschenbild, ISSN 2365-5062, 22.-23.Februar 2022,
URL: https://www.cognitiveagent.org/2022/02/22/popper-wissenschaft-philosophie-oksimo-paradigma/
[6] William Kneale and Martha Kneale, The development of logic, Oxford University Press, Oxford, 1962 with several corrections and reprints 1986.
[7] Jean Dieudonnè, Geschichte der Mathematik 1700-1900, Friedrich Viehweg & Sohn, Braunschweig – Wiesbaden, 1985 (From the French edition “Abrégé d’histoire des mathématique 1700-1900, Hermann, Paris, 1978)
[8] Philip J.Davis & Reuben Hersh, The Mathematical Experience, Houghton Mifflin Company, Boston, 1981
[9] Nicolas Bourbaki, Elements of Mathematics. Theory of Sets, Springer-Verlag, Berlin, 1968
[10] Wolfgang Balzer, C.Ulises Moulines, Joseph D.Sneed, An Architectonic for Science. The Structuralist Program,D.Reidel Publ. Company, Dordrecht -Boston – Lancaster – Tokyo, 1987
[11] The usage of the terms ‘expression’, ‘proposition’, and ‘statement’ is in this text as follows: An ‘expression‘ is a string of signs from some alphabet A and which is accepted as ‘well formed expression’ of some language L. A ‘statement‘ is an utterance of some actor using expressions of the language L to talk ‘about’ some ‘experience’ — from the world of bodies or from his consciousness –, which is understood as the ‘meaning‘ of the statement. The relationship between the expressions of the statement and the meaning is located ‘in the actor’ and has been ‘learned’ by interactions with the world and himself. This hypothetical relationship is here called ‘meaning function φ’. A ‘proposition‘ is (i) the inner construct of the meaning of a statement (here called ‘intended proposition’) and (ii) that part of the experience, which is correlated with the inner construct of the stated meaning (here called ‘occurring proposition’). The special relationship between the intended proposition and the occurring proposition is often expressed as ‘referring to’ or ‘designate’. A statement is called to ‘hold’/ to be ‘true’ or ‘being the case’ if there exists an occurring proposition which is ‘similar enough’ to the intended proposition of the statement. If such an occurring proposition is lacking then the designation of the statement is ‘undefined’ or ‘non confirming’ the expectation.
Follow-up Post
For a follow-up post see here.
