Monthly Archives: August 2022

body-external world, change, change - repeated, change - schema, change rules, difference description, forecasting, Knowledge, meaning, meaning space, measurement, measurement procedure, naive thinking, observational approach, perception, phenomenal space, prediction, rule-compression, sensor signal, time slice

FORECASTING – PREDICTION: What?

eJournal: uffmm.org
ISSN 2567-6458, 19.August 2022 – 25 August 2022, 14:26h
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de

CONTEXT

This text is part of the subject COMMON SCIENCE as Sustainable Applied Empirical Theory, besides ENGINEERING, in a SOCIETY. It is a preliminary version, which is intended to become part of a book.

FORECASTING – PREDICTION: What?

optimal prediction

In the introduction of the main text it has been underlined that within a sustainable empirical theory it is not only necessary to widen the scope with a maximum of diversity, but at the same time it is also necessary to enable the capability for an optimal prediction about the ‘possible states of a possible future’.

the meaning machinery

In the text after this introduction it has been outlined that between human actors the most powerful tool for the clarification of the given situation — the NOW — is the everyday language with a ‘built in’ potential in every human actor for infinite meanings. This individual internal meaning space as part of the individual cognitive structure is equipped with an ‘abstract – concrete’ meaning structure with the ability to distinguish between ‘true’ and ‘not true’, and furthermore equipped with the ability to ‘play around’ with meanings in a ‘new way’.

COORDINATION

Thus every human actor can generate within his cognitive dimension some states or situations accompanied with potential new processes leading to new states. To share this ‘internal meanings’ with other brains to ‘compare’ properties of the ‘own’ thinking with properties of the thinking of ‘others’ the only chance is to communicate with other human actors mediated by the shared everyday language. If this communication is successful it arises the possibility to ‘coordinate’ the own thinking about states and possible actions with others. A ‘joint undertaking’ is becoming possible.

shared thinking

To simplify the process of communication it is possible, that a human actor does not ‘wait’ until some point in the future to communicate the content of the thinking, but even ‘while the thinking process is going on’ a human actor can ‘translate his thinking’ in language expressions which ‘fit the processed meanings’ as good as possible. Doing this another human actor can observe the language activity, can try to ‘understand’, and can try to ‘respond’ to the observations with his language expressions. Such an ‘interplay’ of expressions in the context of multiple thinking processes can show directly either a ‘congruence’ or a ‘difference’. This can help each participant in the communication to clarify the own thinking. At the same time an exchange of language expressions associated with possible meanings inside the different brains can ‘stimulate’ different kinds of memory and thinking processes and through this the space of shared meanings can be ‘enlarged’.

phenomenal space 1 and 2

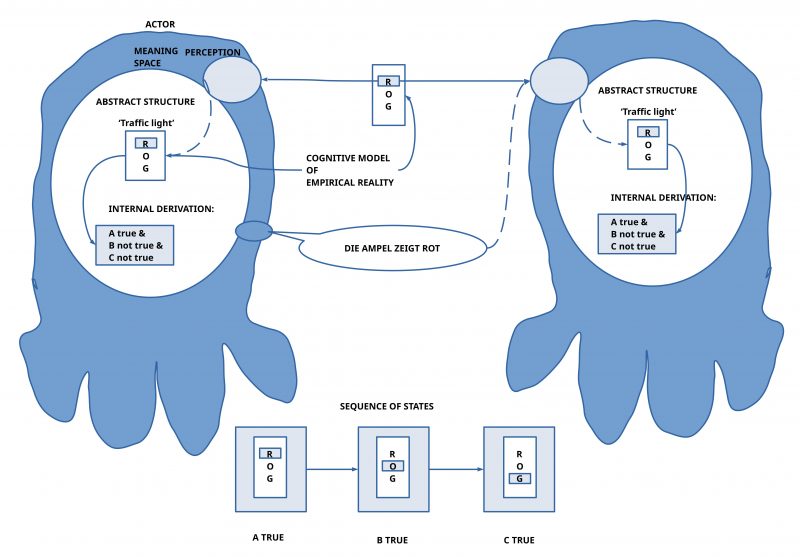
Human actors with their ability to construct meaning spaces and the ability to share parts of the meaning space by language communication are embedded with their bodies in a ‘body-external environment’ usual called ‘external world’ or ‘nature’ associated with the property to be ‘real’.

Equipped with a body with multiple different kinds of ‘sensors’ some of the environmental properties can stimulate these sensors which in turn send neuronal signals to the embedded brain. The first stage of the ‘processing of sensor signals’ is usually called ‘perception’. Perception is not a passive 1-to-1 mapping of signals into the brain but it is already a highly sophisticated processing where the ‘raw signals’ of the sensors — which already are doing some processing on their own — are ‘transformed’ into more complex signals which the human actor in its perception does perceive as ‘features’, ‘properties’, ‘figures’, ‘patterns’ etc. which usually are called ‘phenomena’. They all together are called ‘phenomenal space’. In a ‘naive thinking’ this phenomenal space is taken ‘as the external world directly’. During life a human actor can learn — this must not happen! –, that the ‘phenomenal space’ is a ‘derived space’ triggered by an ‘assumed outside world’ which ’causes’ by its properties the sensors to react in a certain way. But the ‘actual nature’ of the outside world is not really known. Let us call the unknown outside world of properties ‘phenomenal space 1’ and the derived phenomenal space inside the body-brain ‘phenomenal space 2’.

TIMELY ORDERING

Due to the availability of the phenomenal space 2 the different human actors can try to ‘explore’ the ‘unknown assumed real world’ based on the available phenomena.

If one takes a wider look to the working of the brain of a human actor one can detect that the processing of the brain of the phenomenal space is using additional mechanisms:

  1. The phenomenal space is organized in ‘time slices’ of a certain fixed duration. The ‘content’ of a time slice during the time window (t,t’) will be ‘overwritten’ during the next time slice (t’,t”) by those phenomena, which are then ‘actual’, which are then constituting the NOW. The phenomena from the time window before (t’,t”) can become ‘stored’ in some other parts of the brain usually called ‘memory’.
  2. The ‘storing’ of phenomena in parts of the brain called ‘memory’ happens in a highly sophisticated way enabling ‘abstract structures’ with an ‘interface’ for ‘concrete properties’ typical for the phenomenal space, and which can become associated with other ‘content’ of the memory.
  3. It is an astonishing ability of the memory to enable an ‘ordering’ of memory contents related to situations as having occurred ‘before’ or ‘after’ some other property. Therefore the ‘content of the memory’ can represent collections of ‘stored NOWs’, which can be ‘ordered’ in a ‘sequence of NOWs’, and thereby the ‘dimension of time’ appears as a ‘framing property’ of ‘remembered phenomena’.
  4. Based on this capability to organize remembered phenomena in ‘sequences of states’ representing a so-called ‘timely order’ the brain can ‘operate’ on such sequences in various ways. It can e.g. ‘compare’ two states in such a sequence whether these are ‘the same’ or whether they are ‘different’. A difference points to a ‘change’ in the phenomenal space. Longer sequences — even including changes — can perhaps show up as ‘repetitions’ compared to ‘earlier’ sequences. Such ‘repeating sequences’ can perhaps represent a ‘pattern’ pointing to some ‘hidden factors’ responsible for the pattern.

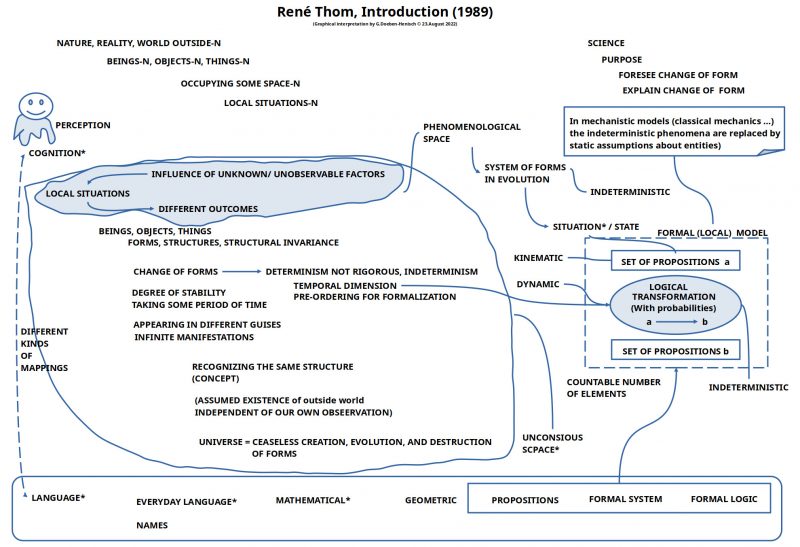
formal representations [1]

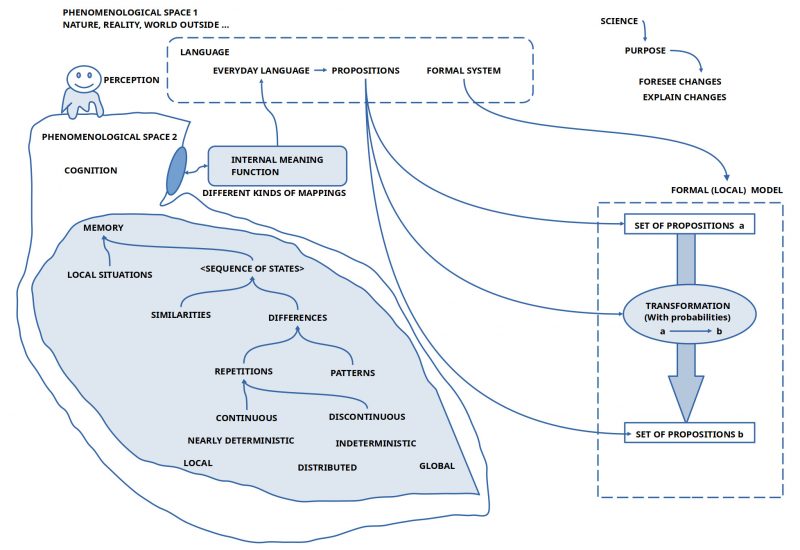
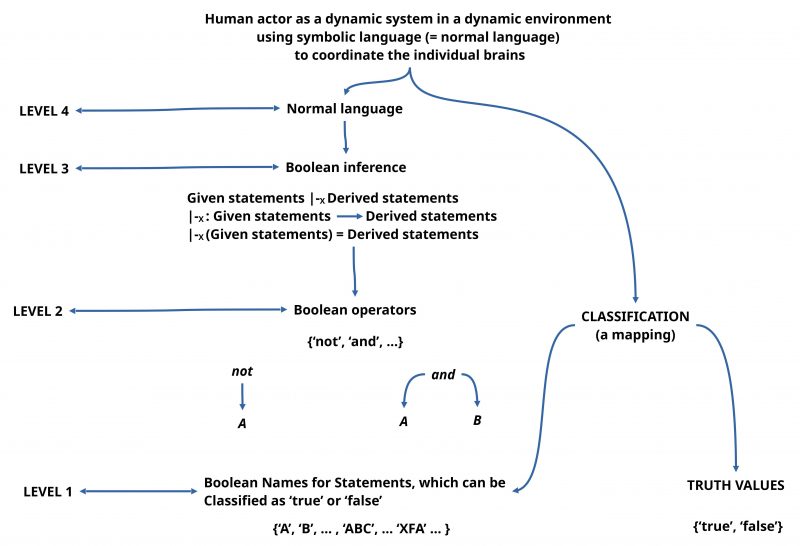
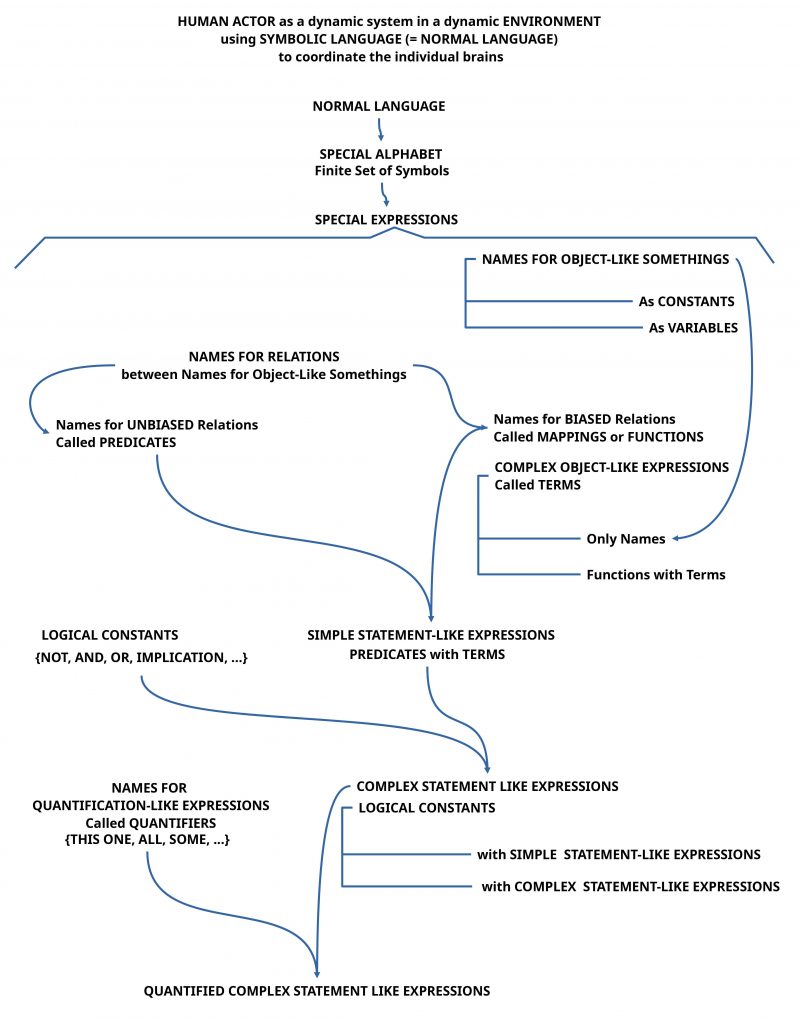
Basic outline of human actor as part of an external world with an internal phenomenal space 2, including a memory and the capability to elaborate cognitive meta-levels using the dimension of time. There is a limited exchange medium between different brains realized by language communication. Formal models are an instrument to represent recognized timely sequences of sets of properties with typical changes.

Based on a rather sophisticated internal processing structure every human actor has the capability to compose language descriptions which can ‘represent’ with the aid of sets of language expressions different kinds of local situations. Every expression can represent some ‘meaning’ which is encoded in every human actor in an individual manner. Such a language encoding can partially becoming ‘standardized’ by shared language learning in typical everyday living situations. To that extend as language encodings (the assumed meaning) is shared between different human actors they can use this common meaning space to communicate their experience.

Based on the built-in property of abstract knowledge to have an interface to ‘more concrete’ meanings, which finally can be related to ‘concrete perceptual phenomena’ available in the sensual perceptions, every human actor can ‘check’ whether an actual meaning seems to have an ‘actual correspondence’ to some properties in the ‘real environment’. If this phenomenal setting in the phenomenal space 2 with a correspondence to the sensual perceptions is encoded in a language expression E then usually it is told that the ‘meaning of E’ is true; otherwise not.

Because the perceptual interface to an assumed real world is common to all human actors they can ‘synchronize’ their perceptions by sharing the related encoded language expressions.

If a group of human actors sharing a real situation agrees about a ‘set of language expressions’ in the sens that each expression is assumed to be ‘true’, then one can assume, that every expression ‘represents’ some encoded meanings which are related to the shared empirical situation, and therefore the expressions represent ‘properties of the assumed real world’. Such kinds of ‘meaning constructions’ can be further ‘supported’ by the usage of ‘standardized procedures’ called ‘measurement procedures’.

Under this assumption one can infer, that a ‘change in the realm of real world properties’ has to be encoded in a ‘new language expression’ associated with the ‘new real world properties’ and has to be included in the set of expressions describing an actual situation. At the same time it can happen, that an expression of the actual set of expressions is becoming ‘outdated’ because the properties, this expression has encoded, are gone. Thus, the overall ‘dynamics of a set of expressions representing an actual set of real world properties’ can be realized as follows:

  1. Agree on a first set of expression to be a ‘true’ description of a given set of real world properties.
  2. After an agreed period of time one has to check whether (i) the encoded meaning of an expression is gone or (ii) whether a new real world property has appeared which seems to be ‘important’ but is not yet encoded in a language expression of the set. Depending from this check either (i) one has to delete those expressions which are no longer ‘true’ or (ii) one has to introduce new expressions for the new real world properties.

In a strictly ‘observational approach’ the human actors are only observing the course of events after some — regular or spontaneous –time span, making their observations (‘measurements’) and compare these observations with their last ‘true description’ of the actual situation. Following this pattern of behavior they can deduce from the series of true descriptions <D1, D2, …, Dn> for every pair of descriptions (Di,Di+1) a ‘difference description’ as a ‘rule’ in the following way: (i) IF x is a subset of expressions in Di+1, which are not yet members of the set of expressions in Di, THEN ‘add’ these expressions to the set of expressions in Di. (ii) IF y is a subset of expressions in Di, which are no more members of the set of expressions in Di+1, THEN ‘delete’ these expressions from the set of expressions in Di. (iii) Construct a ‘condition-set’ of expressions as subset of Di, which has to be fulfilled to apply (i) and (ii).

Doing this for every pair of descriptions then one is getting a set of ‘change rules’ X which can be used, to ‘generate’ — starting with the first description D0 — all the follow-up descriptions only by ‘applying a change rule Xi‘ to the last generated description.

This first purely observational approach works, but every change rule Xi in this set of change rules X can be very ‘singular’ pointing to a true singularity in the mathematical sense, because there is not ‘common rule’ to predict this singularity.

It would be desirable to ‘dig into possible hidden factors’ which are responsible for the observed changes but they would allow to ‘reduce the number’ of individual change rules of X. But for such a ‘rule-compression’ there exists from the outset no usable knowledge. Such a reduction will only be possible if a certain amount of research work will be done hopefully to discover the hidden factors.

All the change rules which could be found through such observational processes can in the future be re-used to explore possible outcomes for selected situations.

COMMENTS

[1] For the final format of this section I have got important suggestions from René Thom by reading the introduction of his book “Structural Stability and Morphogenesis: An Outline of a General Theory of Models” (1972, 1989). See my review post HERE : https://www.uffmm.org/2022/08/22/rene-thom-structural-stability-and-morphogenesis-an-outline-of-a-general-theory-of-models-original-french-edition-1972-updated-by-the-author-and-translated-into-english-by-d-h-fowler-1989/

catastrophe theory, Knowledge, morphogenesis, René Thom, theory of models, topology

René Thom, Structural Stability and Morphogenesis: An Outline of a General Theory of Models (original French edition 1972, updated by the author and translated into English by D.H.Fowler, 1989)

eJournal: uffmm.org, ISSN 2567-6458,
22.August 2022 – 24.August 2022, 17:30h
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de

SCOPE

In the uffmm review section the different papers and books are discussed from the point of view of the oksimo paradigm, which is embedded in the general view of a generalized ‘citizen science’ as a ‘computer aided sustainable applied empirical theory’ (CSAET). In the following text the author will discuss parts of the book “Structural Stability and Morphogenesis: An Outline of a General Theory of Models” from René Thom, originally as a French edition 1972, after several new editions updated in 1988 by the author and translated by H.D.Fowler 1988 into English, published 1989.

CONTEXT

In the foundational post with the title “COMMON SCIENCE as Sustainable Applied Empirical Theory, besides ENGINEERING, in a SOCIETY” a central idea is that a sustainable society has besides the challenge of the right usage of resources the other big challenge related to the ‘cognitive dimension’ as medium of its coordinated actions addressing a sufficiently well prepared planet for the survival of the biosphere in the future. Part of the cognitive dimension is the ability to ‘predict’ a — hopefully — ‘optimal’ course of events leading into the future as a guideline for the life today. It appears to the author of this review that the book of René Thom can give some ‘advice’ for a deeper understanding of the nature of ‘prediction’ using ideas of mathematics, especially ‘topology’ and ‘catastrophe theory’.

Mapping Nature into Formal Models

This figure shows some part of the introduction of René Thom’s book. Look to the text for a comment.

the big picture first

There are multiple ways to approach the ideas of René Thom in his introduction. Let us try an approach coming from the ‘outside’ and then ‘digging into the hidden structures’.

The outside framework is characterized by nature, the ‘real world outside’, by human actors occurring in this world with their bodies, and ‘language communication’ between human actors.

With regard to ‘language’ Thom cites many different ‘variants of language’ besides the ‘everyday language’ like ‘formal logic’, ‘formal systems’, ‘propositions’ etc., but he does not give a systematic account of these different variants; he does not explain the systematic relationships between these different variants.

The inward interaction between the real world outside and a human actor is characterized by ‘perception’. Perception maps properties of the outside world into the inner states of the body, especially into the brain, but Thom never mentions the brain explicitly. These mapped properties from the outside world inside the body are circumscribed for instance as ‘local situations’, ‘beings, objects, things’, ‘change of forms’, ‘degree of stability’, ‘different guises’. But because Thom doesn’t offer some explicit conceptual framework of the ‘inner space’ of a human actor, these concepts have no clear meaning. They only ‘trigger’ in the reader some associations in his everyday language understanding of some possible related meanings without a clear context.

Thom’s remark of a ‘phenomenological space’ remains a bit ‘cryptic’. In science it is common to associate the ‘phenomenological space’ with the way how the ‘world outside’ ‘appears to us’, but — using philosophical reasoning enhanced by brain science and experimental psychology — the properties of the outside world ‘as such’ are not available for the brain in the body. Only the ‘transformation’ of the outside world properties to the different perceptional organs of the body and their processing during ‘perception’ — thereby interacting at least with the memory — enables some ‘neuronal signals’ which are the ‘base ground’ for our brain to ‘compute’ some structures which we are using as ‘phenomena’ in our ‘conscious thinking’. Thus from the point of view of modern philosophy the ‘phenomenal space’ appears to be a space ‘inside the brain’, and this space is accompanied by the ‘unconscious space of cognition’, who is doing the ‘real job’; the ‘phenomenal space’ seems — today — to be a function of this unconscious cognitive space.

Despite the ‘vagueness’ of the descriptive wordings so far Thom introduces more concepts of the ‘inner world’, which seem to be intended as to differentiate the other words a little bit more.

Thus, the ‘infinite manifestations’ of the ‘appearing different guises’ of things can be ‘recognized as the same structure’, or that we ‘assume the existence of the outside world’ ‘independent of our own observation’.

With regard to ‘local situations’ which we can recognize, he reflects about the possible ‘influence of unknown/ unobservable factors’ which can cause ‘different outcomes’, that means different changes in the local situations.

More generally he thinks about the ‘universe’ as a ‘ceaseless creation’, which manifests itself in an ‘evolution’, which is accompanied by a ‘destruction of forms’. The destruction of forms is the same as the ‘change of forms’, which Thom classifies as ‘not rigorous deterministic’, hence ‘indeterministic’. The other aspect of ongoing changes is a ‘temporal dimension’ showing up; translated in a certain kind of ‘ordering’ these changes can be ‘translated’ into a formalization as a succession of states. Each state will be represented by a ‘set of properties’. With the aid of some logical inference mechanism it is possible to ‘transform’ one set of properties into another set of properties, including a measure for the probability, that the next set of properties will be inferred.

While the real world as such appears to us as some infinite source of phenomena with an unknown number of hidden factors are the elements of the outside world in general somehow infinite and indeterministic in their occurrence. But a human actor looking into this phenomenal space he can decide to assume the open character of phenomena as being describable as clear-cut finite things — as in ‘classical mechanics’ –, which allows a ‘deterministic’ handling of the phenomena. With other conceptual strategies — like in ‘quantum mechanics’ — the primary phenomena are classified as ‘indeterministic by nature’ which translates into logical inferences which are also ‘indeterministic’.

The overall purpose of science sees Thom as given in the intention to ‘foresee change of form’ and to ‘explain change of form’.

observables – local models – ultimate natuRe of reality

Thom points out that finally for a ‘macroscopic description of a system’ only the ‘observables’ of a local system are available.(cf. p.6f) What is ‘behind’ these observables, what exactly has to be understood by the ‘ultimate nature of reality’, this cannot completely be covered by a local system, by no local system.(cf. p.6f) Whether all local systems can finally be integrated into one coherent global system is an open question.(p.7)

a mathematics of discontinuities?

Thom considers further the fact that in common everyday experience we encounter many phenomena which appear in themselves to be very trivial but which are opposing a simple mathematical description.(cf. p.9) The main characteristic of these everyday phenomena is ‘discontinuity’. Because all applicable quantitative mathematical models rely on ‘continuity’ and ‘continuous functions’ this reduces the probability that science starts to describe ‘discontinuity’.(cf. p.9) Nevertheless there are more and more disciplines which are confronted with ‘discontinuous’ phenomena, which are ‘unstable’, show nearly ‘no repetition’ and do not fit easily in a mathematical model.(cf. p.9)

Thom gives a short outline of an idea how to cope with discontinuity by constructing a model of a set M of ‘observables’ which as such are ‘stable’, but they include a closed subset K of ‘catastrophes’ which manifest themselves as ‘singularities’ provoking a ‘discontinuity’ which can cause a ‘change’ on the observables, which constitutes the global phenomenon of ‘morphogenesis’.(cf. p.7) By not knowing in advance the ‘dynamics’ X underlying these changes it is possible to ‘reconstruct’ (step-wise) the underlying dynamics X by observing the global morphogenesis by recurring to the local changes too.(cf. p.7)

Thom underlines that it is not the local singularity as such which manifests the underlying dynamics X but the ‘accumulation’ of all singularities into ‘one global phenomenon’, which has to be explained.(cf. p.8) And because the ‘statistics’ of the local changes, which can be correlated with the local accidents, is determined by the underlying dynamics, it will not suffice to rely only on a local change; all changes together have to be explained. This can imply more than three dimensions of an euclidean space.(cf. p.8)

Discussion of Thom’s Position

There are some aspects which could be discussed in front of Thom’s position.

One major point could be his ‘vagueness’ with regard to the inner structure and processing of a human actor. Since 1972 (1989) many new deep insights have been revealed by disciplines like brain sciences in connection with experimental psychology and biology. I will not discuss this point here. There are several posts in the uffmm.org blog which are dealing with these topics.

What catches the attention of the reviewer here is the position of Thom considering the phenomenon of ‘discontinuities’ (changes) which not as a ‘single change’ represent a phenomenon but as a ‘series of changes’ which can not be classified as a ‘classical quantitative continuous’ phenomenon.

He thinks that especially ‘topological thinking’ can be of help here.

Comparing Thom’s position with the position of the the concept of a ‘sustainable empirical theory’ as it is outlined in the uffmm.org blog, especially condensed as a ‘theory producing process’ called ‘oksimo-R process paradigm’, it seems to be not only possible to solve the problem without topology, but — perhaps — even better without topology.

This results from the fact that the oksimo-R process paradigm presupposes a conceptual framework where not only the human actor as ‘theory producer’ is assumed to be located with his body in a ‘body-external empirical world’, but there exist also some additional assumptions about the ‘internal structure’ and the ‘internal processing’ of human actors, which are ‘explaining’ to a certain degree how a human actor can process properties of his environment — including his own body — within a cognitive and emotional space as well how he can ‘map’ parts of these spaces into sets of expressions of his everyday language. Based on such a ‘process model’ of a human actor it is possible to ‘explain’ additionally the language-based communication between different human actors whereby the different brains in the bodies can share some knowledge and emotions and can coordinate their actions.

The concept of a formal model which Thom introduced before can in the light of a more advanced actor model be interpreted in a way, that it allows all the solutions which Thom claims for his topological minded approach.

Which series of ‘changes’ (maybe ‘catastrophes’) will attract the attention of some researchers, the researcher are every time capable to do the following:

  1. Write a series of texts representing the observed phenomena at location L and time T in accordance with their learned and agreed meaning functions (a set of propositions).
  2. This will result in a series of texts (documents) <D1, D2, …, Dn>, whose logical ordering represents the timely order.
  3. Because every ‘difference’ between two consecutive documents (Di,Di+1) is directly observable in the language expressions one can ‘translate’ these differences directly by a rule following a general format: (i) IF x is a subset of expressions in Di+1, which are not yet members of the set of expressions in Di, THEN ‘add’ these expressions to the set of expressions in Di. (ii) IF y is a subset of expressions in Di, which are no more members of the set of expressions in Di+1, THEN ‘delete’ these expressions from the set of expressions in Di. (iii) Construct a ‘condition-set’ of expressions as subset of Di, which has to be fulfilled to apply (i) and (ii).
  4. After the translation of all observed differences between consecutive documents one has a set of ‘change rules X’, which together with the ‘Start Document’ D0 define an ‘accumulated rule’ for a series of discontinuous changes: <D0, X>

Probably a first ‘guess’ of an accumulated rules will be not too ‘precise’. Thus by collecting more ‘observations’ one can try to ‘refine’ the rules, even including local probabilities, which during ‘processing’ (inference, simulation) can produce an ‘accumulated and composed’ probability of some ‘weird’ kind.[1]

COMMENTS

[1] This view of composed probabilities is in a good agreement with the ideas of the late Karl Popper discussing ‘propensities’ (see several posts in this uffmm.org blog: https://www.uffmm.org/2021/03/15/philosophy-of-science/)

Chapter

Language

eJournal: uffmm.org
ISSN 2567-6458, 19.August 2022 – 19 August 2022
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de

CONTEXT

This text is part of the subject COMMON SCIENCE as Sustainable Applied Empirical Theory, besides ENGINEERING, in a SOCIETY. It is a preliminary version, which is intended to become part of a book.

Language

The words ‘science’, ‘theory’, and ‘scientific theory’ are well known passengers travelling through the times with different meanings, depending from the circumstances, from the minds of different people.[2]-[4] In modern times we have learned a lot about the nature of ‘signs’ and ‘sign-based’ communication as it happens when we are using a ‘language’. And, becoming more sensitive about the dynamics of sign-based communication, we can detect that it is exactly our human use of language which provides the key to a deeper understanding of how our brains are working, located in our bodies, where the brains are playing the roles of ‘spin doctors’ of the pictures in our heads, which are ‘showing’ our mind a ‘virtual world’ of an assumed ‘real world’ somewhere ‘out there’.[14]

Until today we have no final explanation of how exactly this ability of human actors has developed through the times stretching to millions of years ago. And until today there exists no complete description of a living language with the involved structures, meanings, and dynamics. One reason for this ‘fundamental inability’ of describing with a language exactly this language roots is the fact, that language is not a ‘single fixed object’ in front of your eyes, but a dynamic reality happening between many, many different human actors simultaneously; every brain has only some fragments of this assumed ‘whole thing’ called ‘language’, and every communicative act between humans embraces besides ‘rather stable parts’ always a lot of ‘incidental’, ‘casual’ moments of a complex dynamic situation, which constitutes — mostly unconscious — the working of language communication, possible meanings and connotations of meaning. Thus, all the known scientific endeavors until today trying to describe this phenomenon of language communication are more reminding some ‘stuttering’ than a final ‘ordered’ theory.

One lesson we can learn from this tells us, that the so-called ‘everyday language’, the ‘ordinary language’, the ‘natural language’ is the ‘basic’ pattern of language communication. But, as mentioned just before, on account of the fundamental distributed and dynamical character of everyday language, a natural language has no clear cut ‘boundaries’. Never you can tell with certainty where a language ends and where this language just in that moment ‘evolves’, ‘expands’, is ‘changing’.

For people which are looking for ‘clear statements’, for ‘finite views’, for a ‘stable truth’ this situation is terrifying. It can cause ‘anxious feelings’. People who like to ‘control’ life don’t like such a ‘living dynamics’ which can not be owned by a single person alone, not even by ‘many’…

One basic property of ordinary language is it’s ‘expandability’: at every time someone can introduce new expressions embedded within new contexts following new patterns of usage. If other human actors start to follow this usage, this ‘new’ behavior is ‘spreading’ through the ‘population of language users’ and by this new growing practice the ordinary language is expanding and thereby changing.

One ‘part’ of ordinary language is called ‘logic’ [6],[7], with various different realizations through history. Another part of ordinary language is ‘mathematics’, especially what is today assumed as being the ‘kernel’ of mathematics, the ‘Theory of Sets’.(cf. [8], [9]) Because ordinary language can always be used to speak ‘about ordinary language’, it is possible to extend an ordinary language with arbitrary many new ‘artificial languages’ like a ‘logic language’ or a ‘mathematical language’.[10] After introducing a special language like a mathematical language’ by using ordinary language one can apply this special language ‘as if it is the only language’, but if you start to ‘look consciously’ to your real practice of speaking, you can easily detect, that this impression ‘it is the only language’ is a fake! Cutting away the ordinary language you will be lost with your special language. The ordinary language is the ‘meta language’ to every special language. This can be used as a ‘hint’ to something really great: the mystery of the ‘self-creating’ power of the ordinary language which for most people is unknown although it happens every moment.

— draft version —

Chapter

Concrete Abstract Statements

eJournal: uffmm.org
ISSN 2567-6458, 19.August 2022 – 19 August 2022
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de

CONTEXT

This text is part of the subject COMMON SCIENCE as Sustainable Applied Empirical Theory, besides ENGINEERING, in a SOCIETY. It is a preliminary version, which is intended to become part of a book.

Concrete – Abstract Statements

From the everyday language we know that we can talk ‘about the world’, and even more, we can even ‘act’ with the language. [11] – [13] Saying “Give me the butter, please”, in that case a ‘normal’ [*2] speaker would ‘hear’ the ‘sound of the statement’, he can ‘translate the sound’ into some internal meaning constructs related to the sounds of the language, which in turn will — usually — be ‘matched against’ meaning constructs ‘actually provided’ by the ‘perception’. If there happens to be a ‘sufficiently well match’ then the hearer can identify ‘something concrete’ located on the table which he can associate with the ‘activated language related meaning’ and he then ‘knows’, that this concrete something on the table seems to be an ‘instance’ of those things which are called ‘butter’. But there can exist many different ‘concrete things’ which we agree to accept as ‘instances’ of the meaning construct ‘butter’. Thus, already in very usual everyday situations we encounter the fact, that our perceptions can create signals from ‘something concrete in our perceptions’ and our ‘language-mediated understanding’ can create ‘meaning structures’ which can ‘match’ nearly uncountable different concrete things. [*3] Those meaning constructs — activated by the language, but different from the language — which can match more than one concrete perception, will here be called ‘abstract meaning’ or ‘abstract concept’. And ‘words’ (= expressions) of a language which can activate such abstract meanings are understood as ‘abstract words’, ‘general words’, ‘category words’ or the like. [*4]

Knowing this you will probably detect, that nearly all words of a language are ‘abstract words’ activating ‘abstract meanings’. This is in one sense ‘wonderful’, because the real empirical world consists of uncountable many concrete perceivable properties and to relate every concrete property with an individually matching word would turn the project of language into an infeasible task. Thus with only a few abstract words language users can talk about ‘nearly everything’. This makes language communication possible. The ‘dark side’ of this wonderful ability is the necessity to provide real situations, if you want to demonstrate which of all these concrete properties of a real situation you want to be understood as ‘related’ to the one used word (= language expression) with an abstract meaning. If you cannot provide such ‘concrete situations’ the intended meaning of your abstract words will stay ‘unclear’: they can mean ‘nothing or all’, depending from the decoding of the hearer.

— draft version —

Chapter

True – False – Undefined

eJournal: uffmm.org
ISSN 2567-6458, 19.August 2022 – 19 August 2022
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de

CONTEXT

This text is part of the subject COMMON SCIENCE as Sustainable Applied Empirical Theory, besides ENGINEERING, in a SOCIETY. It is a preliminary version, which is intended to become part of a book.

True – False – Undefined

Talking about ‘butter’ on ‘tables’ during a ‘breakfast’ will usually stimulate lots of ‘imaginations’ in the head of the hearer of such utterances. Because an abstract word can trigger many different ‘concrete things’ these individual imaginations can vary a lot. If different hearers would start to ‘paint’ those imaginations on some paper it could happen, that nearly no two paintings would ‘match’ with all details. The ‘space of possible meanings’ of an abstract word (‘butter’, ‘table’, ‘breakfast’, ‘kitchen’, …) is in principle ‘infinite’. And the manifested ‘diversity’ of the details reveals a kind of ‘fuzziness’ which at a first glance seems to be ‘infeasible’ in the practice of language communication.

This appearing diversity, fuzziness in the examples points to some ‘internal mechanism’ in our brains which works in complete ‘silence’, always ‘automatically’, completely ‘unconscious’, which ‘arranges’ the many different perceptions in a way, which selects some finite set of properties out of the many perceived properties and makes such a ‘selection’ to a kind of ‘signature’, ‘address’, which starts to play the ‘role’ of an individual representation for all those possible sets of perceived properties in the future, which are ‘sufficiently well’ ‘similar’ to those ‘signature properties’. The ‘boundaries’ are not sharp; the boundaries can vary; there can grow large ‘clusters of different property sets’ intersecting with this ‘signature set’ but are different otherwise. Thus, there exists a growing meaning structure in our brains which creates a ‘meaning space’, whose elements can be associated in arbitrary many ways.

If my friend Bill starts talking with me by asking whether there already is some butter on the table, than his utterance — a question — will trigger in me a subset of possible meanings of butter which are in my memory available. Then, when I am looking to the table in the kitchen, I will ‘scan’ the table whether there is something concrete which will ‘match’ these activated internal meanings. Either there happens a direct match or there is something, which looks like something, which feeds back through my perception and urging my memory to ‘look for something alike’. If this happens, then there will be a match too. Thus if such an internal match between ‘perceived properties’ and ‘remembered properties’ will happen then I would shout to Bill “Yes, there is already some butter on the table”. If no such match would happen, then I would shout back “No, there is not yet butter on the table”. In the first case we are used to classify a statement as ‘true’, if the abstract meaning matches a concrete perception sufficiently well; otherwise not. If Mary standing nearby the table would have said before “No, there is no butter on the table” while Jeremy has stated that there is some butter, then these two statements would ‘contradict’ each other. If Jeremy and Mary can come to a common opinion by observable evidence that there is some butter on the table or not, they would be able to ‘agree’ to the positive, affirmative statement that there is some butter on the table, otherwise not. To classify a statement as being ‘false’ would presuppose that the contradicting format of this statement is classified as being ‘true’. If the human actors can not come to a sufficient agreement whether either the statement “Yes, there is already some butter on the table” is true or “No, there is no butter on the table”, then both statements are ‘undecidable’ by the human actors with regard to some observable evidence. In that case these statements are with regard to being ‘true’ or ‘false’ ‘undefined’.[*5]

This everyday situation offers some more variants. If for instance Bill is asking Jeremy whether there is some butter on the table it could happen either that Jeremy says ‘no’ because his ‘understanding’ of the word ‘butter’ consist of kinds of meaning which are not matching that concrete thing on the table, which Bill would understand as ‘butter’. Such a ‘misunderstanding’ can happen easily if people from different cultures are coming together. Thus, having some observable evidence does not guarantee the right classification within a certain language if the language users have learned ‘different meanings in their memory’. In the other case, if Mary has a bad visual perception on account of some ‘visual handicap’ but has in principle the same meaning space like Bill, then it can happen too that she would deny that there is some butter on the table because her visual perceptions are ‘disturbed by their visual handicap’ in a way that the perceptional key to her memory is not in that format which has to match their remembered language induced meaning.

Thus, in this simple example of a ‘true’ statement there are already several ‘factors’ needed to make a ‘true statement’: (i) a perception which works ‘normal’; (ii) a language meaning which is ‘sufficiently common’; (iii) a ‘successful match’ between an actual observation and the triggered memory based meaning. Every factor (i) – (iii) is not simple, can vary a lot. And there exists even more factors which can influence the final classification of being ‘true’ or not; in cases of ‘contradicting statements’ all these different factors can be involved.

In our times of ‘growing fake news’ we can experience, that the agreement between different human persons about the ‘truth’ of a statement can in practice be very difficult or even seems to appear impossible. This points to one more factor which is finally decisive: whatever we perceive and remember, these processes are ’embedded’ in some larger ‘conceptual frameworks‘, which are further ’embedded’ in a system of preferences’ which can be ‘decisive’ for the ‘handling’ of our opinions. Human persons having certain ‘convictions’ related to political or religious or ethical opinions can be ‘driven’ by these convictions in a way, which ‘overrides’ empirical evidences because their ‘conceptual frameworks’ ‘interpret’ these perceptions in a different way. Modern scientific observations are meanwhile often in a format, which only experts can interpret adequately related to a ‘theoretical conceptual framework’. If a non-expert does ‘not trust’ in this scientific interpretation he can ‘switch’ to a different conceptual framework in which he is trusting more, although this other concepOrdinary Language Inference: Preserving and Creating Truthtual framework contradicts the scientific framework, and thus he can assume ‘facts’ which are contradicting those ‘facts’ classified as scientific. Scientists can classify these other facts as ‘fake news’, but this will have no effect on the believer of the fake news. The fake-news believer thinks he is ‘right’ because it matches his individual framework shared by others in social groups.

From this follows that the classification of a statement as being ‘true’ is a complex matter depending from many factors which have to be ‘synchronized’ to come to an agreement. Especially it reveals that ’empirical (observational) evidence’ is not necessarily an automatism: it presupposes appropriate meaning spaces embedded in sets of preferences, which are ‘observation friendly’.

— draft version —

Chapter

Beyond NOW

eJournal: uffmm.org
ISSN 2567-6458, 19.August 2022 – 19 August 2022
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de

CONTEXT

This text is part of the subject COMMON SCIENCE as Sustainable Applied Empirical Theory, besides ENGINEERING, in a SOCIETY. It is a preliminary version, which is intended to become part of a book.

Beyond NOW

Every (biological) system which has some sensory input possesses certain states which represent for the system the NOW: that what ‘happens actually’, what is ‘present’ in a mixture of properties and events.

But a NOW provides as such no ‘knowledge’. It is only a NOW.

To ‘overcome’ the NOW a system must be able to map parts of the NOW into other systems states, into such states, which can be ‘recalled’, and which as ‘recalled states’ can be ‘compared’ with the actual NOW. Such a ‘comparison’ can yield ‘similarities’ and ‘differences’. Out of differences distributed over different recalled states ‘sequences of states’ can be constructed’, and sequences of such states can reveal by differences ‘changes’ of properties between consecutive states. With the aid of such sequences revealing possible changes the NOW is turned into a ‘moment’ embedded in a ‘process’, which is becoming the more important reality. The NOW is something, but the PROCESS is more.

— draft version —

Chapter

Playing with the Future

eJournal: uffmm.org
ISSN 2567-6458, 19.August 2022 – 19 August 2022
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de

CONTEXT

This text is part of the subject COMMON SCIENCE as Sustainable Applied Empirical Theory, besides ENGINEERING, in a SOCIETY. It is a preliminary version, which is intended to become part of a book.

PLAYING WITH the FUTURE

In this enlarged reality of a process the ability to generate ‘signatures’ representing ‘some properties’ out of a set of properties, is the other ‘magic’ tool to compose ‘abstract structures’ which can be expanded if necessary, which can be related to nearly everything; an abstract structure can become associated with other structures, can be embedded in ‘hierarchic’ structures, and even more. Abstract structures are the other ‘tools’ to overcome the NOW: ‘reality’ is not only ‘what is now’, but in the same time also that what can be added, extended, combined to the given structure. Abstract structures are as part of an embracing process ‘potentials’, ‘possible alternatives’, something which can become ‘true’ in some following state, that means in some ‘possible future.’

If someone has introduced the word ‘cup’ for something concrete which allows to hold some fluid, which can be used to ‘drink’ out of this concrete something, the word ‘cup’ — an expression of some language — is not a fixed, static object but — as part of a possible process — can be used to ‘touch’ more and more different concrete objects allowing them to become ‘part of the internal meaning structure’ of a speaker-hearer. Thus while the ‘word’ as language expression stays ‘the same’ the associated meaning space can change, can grow, can shrink, can be associated with other meaning spaces.

In this sense seems ‘language’ to be the master tool for every brain to mediate its dynamic meaning structures with symbolic fix points (= words, expressions) which as such do not change, but the meaning is ‘free to change’ in any direction. And this ‘built in ‘dynamics’ represents an ‘internal potential’ for uncountable many possible states, which could perhaps become ‘true’ in some ‘future state’. Thus ‘future’ can begin in these potentials, and thinking is the ‘playground’ for possible futures.(but see [18])

— draft version —

Chapter

FORECASTING

eJournal: uffmm.org
ISSN 2567-6458, 19.August 2022 – 20 August 2022
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de

CONTEXT

This text is part of the subject COMMON SCIENCE as Sustainable Applied Empirical Theory, besides ENGINEERING, in a SOCIETY. It is a preliminary version, which is intended to become part of a book.

FORECASTING

(Has to be re-written)

We know from everyday life and partially from science that this ability of abstract potentials as part of possible processes can under certain conditions be used for ‘forecasts’ with important practical consequences: for the Egyptian people it was of high importance to know in advance when the floods of the Nil river would arise again. Generally it was important to understand the different periods of the year, the process of time, or the connections between food and effects on our bodies, or the ‘art of agriculture’ to prepare for enough food for all people, and much more.

With the reality of being part of a process with a NOW, with the ability to overcome the NOW by generating abstractions, sequences of states, and recognizing changes, with the ability to derive ‘possible follow-up states’ out of the known sequences of states, it is generally possible to produce forecasts.

But not any forecast is ‘helpful’.

If the experts say that in two weeks the floods of the river will come, but this would not happen, it would not be appreciated; if people recommend certain food for your health and you will become ill, it would not be appreciated either. Thus forecasts should possess the property, that the state, which is ‘announced to become true’, indeed would become ‘true’. ‘True’ means here that the ‘announced state’ will at some ‘point in the future’ be ‘instantiated by some real facts which can be observed.

This leads to the interesting question, how it is possible to ‘derive’ from some ‘given states’ in the memory ‘possible states’ in the memory, which have the potential to become in some time ‘instantiated’ in a way, which makes them ‘real’ and thereby ‘observable’.

In modern formal logic language expressions are well defined expressions of some language but ‘without any concrete meaning’. The only assumed property of logical statements is the property to be called ‘true’ or ‘false’ without relating these abstract properties to some real meaning. Thus you can play with these ‘logical expressions’ in a purely formal way by defining some rules, how one can change an expression and under which conditions the transformation of a set of given expressions into another set of expressions is called a ‘logical derivation’ which preserves the ‘abstract trues’ of the assumed primary set of expressions. These are nice games allowing numerous different kinds of definitions of ‘logical derivation’ without any real relation to everyday language and meaning. All the known examples how to use formal logic applied to everyday meaning until today are not really convincing. The numerous articles and even books dealing with such examples can only work, if we forget nearly everything which we know about our everyday world. This seems to be a strange deal.

If one instead looks to the way human actors are making forecasts in the everyday world without using formal logic one can detect, that this is not only possible, it seems to be the only powerful way to do it.

— draft version —

Chapter

THE LOGIC OF EVERYDAY THINKING. Lets try an Example

eJournal: uffmm.org
ISSN 2567-6458, 19.August 2022 – 19 August 2022
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de

CONTEXT

This text is part of the subject COMMON SCIENCE as Sustainable Applied Empirical Theory, besides ENGINEERING, in a SOCIETY. It is a preliminary version, which is intended to become part of a book.

THE LOGIC OF EVERYDAY THINKING

In the following examples four languages are used simultaneously: (i) Boolean logic, (ii) German language, (iii) English language, (iv) Predicate logic. The idea is to make ‘visible’ that formal logic provides not only a very limited profit, but that the normal language can offer all what formal logic can offer, but even much more. If one keeps in mind that the ‘normal’ language is principally the meta-language for every kind of ‘special’ language then this should be no surprise.

— draft version —

Chapter

Boolean Logic

eJournal: uffmm.org
ISSN 2567-6458, 19.August 2022 – 19 August 2022
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de

CONTEXT

This text is part of the subject COMMON SCIENCE as Sustainable Applied Empirical Theory, besides ENGINEERING, in a SOCIETY. It is a preliminary version, which is intended to become part of a book.

Boolean Logic

Figure: Outline of boolean logic from the perspective of language usage by human actors.

In the language of boolean logic — also called ‘propositional logic’ (but see [17]) — we have only expressions for ‘names’ of statements — like ‘A’, ‘B’, ‘CD’, … — , which can be classified (on a meta-level!) as being ‘true‘ or ‘false‘.

Whether one of the used names for statements is ‘true’ or ‘false’ has to be explained ‘separately’ — on a meta-level! — often written in a list or table called ‘truth table’ like:

  1. A, true
  2. B, false
  3. C, false

Further we have some expressions naming ‘logical operators’ which we write here as ‘not‘ and ‘and‘. Strictly speaking these are on a ‘meta-level’ compared to the expressions representing statements which can be true or false.

Thus we could write the compound statement ‘A and B and C’

claiming that the whole expression has the meta-property of being true independent which truth values the individual statement expressions B’ and ‘C’ are assumed to have.

This simultaneous occurrence of two different meta-levels in the description of boolean logic expressions raises the question, how these metal-levels are ‘interacting’? The discussion of this question will be postponed here until we have discussed what is called a ‘logical derivation’.

A ‘logical derivation rule’ tells us that if we have an expression like ‘A and B’ ‘assumed’ to be ‘true’ than we can ‘derive’ from this expression that the expression ‘A’ or ‘B’ alone is also ‘true’. Thus with our introductory example, that the expression A and B and C is assumed to be true, we could ‘logically derive’ that the expressions A, or B, or C taken ‘alone’ are true either. In the logical meta-language we could describe this derivation relation as

A and B and C  ⊢X A

or

A and B and C  ⊢X B

or

A and B and C  ⊢X C

where the sign ⊢X denotes the logical derivation operator (meta-level !) with the arguments (left side) A and B and C and (right side) A or B or C. The index sign ‘X’ represents the set of derivation rules. In this case we have only one rule, therefore X = {if we have an expression like ‘A and B’ ‘assumed’ to be ‘true’, than we can ‘derive’ from this expression that the expression ‘A’ or ‘B’ alone is also ‘true’}

Coming back to the question of the interplay between the meta-level assumption that the expression C is assumed to be false but can be derived from the compound statement A and B and C as being ‘true’ reveals that the property of being ‘false’ of an individual statement and the property of an individual statement ‘C’ to be in a logical derivation ‘true’ describes apparently two different properties.

A possible solution of this meta-problem can be to introduce the convention, that the ‘individual true-false qualification’ can be expressed by ‘C’ as encoding ‘C is true individually’ and ‘not C’ as encoding ‘C is false individually’. But this ‘convention’ will only work if it would be ‘done’ before’ a logical derivation (again a meta-level matter). Thus, if one assumes the individual true-false qualifications of the before mentioned truth-table as ‘given’, than we had to write the compound statement as

A and not B and not C

which could yield the following derivations

A and not B and not C  ⊢X A

or

A and not B and not C  ⊢X not B

or

A and not B and not C ⊢X not C

Thus we have presupposed ‘individual truth values’ and then one can logically derive either ‘B’ or ‘not B’ as ‘logically true’.

This discussion of ‘individual truth values’ compared to ‘logically derived truth values’ raises confusion. Indeed, boolean logic as such takes only names for expressions like ‘A’ or ‘B’ as arguments for their logical operators — ‘not’, ‘and’, … — being fed into a logical derivation relation — ⊢X — without taking into account individual truth values. This part is ‘delegated’ to the user of boolean logic; the possible ‘interpretation’ of boolean logic expressions’ with ‘real truth’ is ‘outside of boolean logic’!

The leading idea is therefore that the usage of a symbolic language has to be understood as an interaction of several ‘levels of meaning’ simultaneously. One single language expression can be seen from the perspective of ‘meaning’ (the adaptive built function in every human actor) as having several ‘levels of meaning’. In the case of boolean logic this are at least four levels.

More aspects of the case of boolean logic will be discussed in the following sections.

— draft version —

Chapter

Everyday Language: The German Example

eJournal: uffmm.org
ISSN 2567-6458, 19.August 2022 – 19 August 2022
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de

CONTEXT

This text is part of the subject COMMON SCIENCE as Sustainable Applied Empirical Theory, besides ENGINEERING, in a SOCIETY. It is a preliminary version, which is intended to become part of a book

EVERYDAY LANGUAGE: GERMAN EXAMPLE

Figure: Simple outline of basic interactions between an empirical object with properties embedded in a situation and (human) actors with perception, meaning space, abstract structures functioning as cognitive models of possible real world somethings. An abstract structure usually includes more than one possible empirical situation thereby ‘transcending’ a perceptional ‘NOW’ into different possible (cognitive) states (encoding possible ‘future’ states). The internal meaning space with its manifold abstract structures allows lots of ‘logical derivations’ which are impossible looking only to utterances or to actual empirical settings.

In the following example we have a human actor being part of a traffic situation, who gives some fragments of a language description of what he is experiencing (in the next section this example will be given with the English language).

In a first situation the human actor would say:

“Die Ampel zeigt rot.”

Some seconds (or minutes) later he would state:

“Die Ampel zeigt orange.”

Again, after some seconds (or minutes) he would utter:

“Die Ampel zeigt grün.”

Then he would start to move away.

We could ‘name’ these expressions by abbreviation in the following way:

A := “Die Ampel zeigt rot.”

B := “Die Ampel zeigt orange.”

C := “Die Ampel zeigt grün.”

In the everyday situation where these statements will be uttered by a human actor this human actor would classify each statement as ‘being true’, because the ‘known meaning’ associated with these expressions is in that moment of being uttered in a ‘sufficient accordance’ with the perceived situation. Thus, one could classify the individual statements as ‘true’ while being ‘uttered’.

Using the abbreviations ‘A’, ‘B’, and ‘C’ we could apply the inference machinery of the boolean logic with

(1) A and B and C  ⊢X A or … B … or C

In the everyday situation where these statements have been uttered this logical inference would be wrong. If we would do it like in (1).

The reason for this insufficiency is grounded in the fact, that each statement from ‘A’, ‘B’, and ‘C’ is describing the property of a traffic light (being red, orange or green), and only one of these statements can be true at a certain point of time. Thus the ‘truth’ of these statements is ‘time dependent’! Furthermore works the traffic sign in an ‘action pattern’ which makes one ‘color’ ‘true’ and at the same time all other colors ‘false’. Thus a traffic light is a collection of statements like this:

(2) traffic light := {‘A and non B and non C’ or ‘non A and B and non C’ or ‘non A and non B and C’} (with ‘or’ as another boolean operator).

From this the following boolean derivations would be possible:

  • One of these statements can become true
  • If e.g. ‘A and non B and non C’ would become true, then one could derive that ‘A’ is true or ‘non B’ or ‘non C’. This would describe the case, where in the everyday world the red sign of the traffic light would be shining.

From the boolean derivation as such it would not be possible to decide, which of the possible variants would be the case in a certain moment. Because boolean logic in general has to assume a human actor (or any kind of actor with sufficient properties), who is able to associate the expressions with his internal meaning space, combined with the intention to classify which of the ‘logically possible variants’ is matching an ‘actual situation’, which offers those ‘meaning properties’, which are needed, to ‘make the expression an instance’ of this meaning case.

Naturally, it is a human actor who has to ‘invent’ the definition of a ‘traffic light’ in the format of (2), if he knows concrete examples of traffic lights in everyday situations. Because of this, because a human actor has an internal knowledge space with an internal meaning function μ, he ‘knows’ which kinds of properties are ‘related’ to that what is called a ‘traffic light’. And from this follows with ‘normal logic’ that

  1. If a traffic light shows a certain color, this is only valid in a certain time span (t,t’) and all the other colors of this traffic light are not active simultaneously.
  2. Thus uttering the statement ‘Die Ampel zeigt rot’ implies that this statement is true in that moment.
  3. By ‘normal logic’ every human actor — with the same meaning space — ‘knows implicitly’ that the other lights do not show their colors in that moment. To make the additional statements that ‘Die Ampel ist nicht gelb’ and ‘Die Ampel ist nicht grün’ are not necessary because every human actor would ‘derive’ these consequences ‘internally purely automatically’ (because our brains work in this fashion without explicitly asking whether they are allowed to do this).

— draft version —

Chapter

Natural Logic

eJournal: uffmm.org
ISSN 2567-6458, 19.August 2022 – 19 August 2022
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de

CONTEXT

This text is part of the subject COMMON SCIENCE as Sustainable Applied Empirical Theory, besides ENGINEERING, in a SOCIETY. It is a preliminary version, which is intended to become part of a book.

Natural Logic

The foregoing comparison of derivations in a ‘boolean logic setting’ and in an ‘everyday language setting’ shows a remarkable difference: while the inventors of boolean logic focused on formal expressions only by cutting of all ‘natural meaning’, the ‘inventor’ of natural language — the whole biosphere! — created ‘normal language’ to be a ‘medium’ to encode the ‘internal states’of the sending brain into expressions which can be transmitted to other brains which as ‘receivers’ should be able to ‘decode’ these expressions into the internal states of the receiving brains. Thus ‘expressions as such’ are of nearly no help for the survival of brains. Survival needs cooperation between different brains and the only chance to enable such cooperation is communication of internal states by ‘encoded expressions’.

From this follows that ‘natural logic’ has to follow completely different patterns than ‘boolean logic’. Let us look to the example again.

We continue using the before introduced abbreviations A := ‘Die Ampel zeigt rot’ etc.

In figure 3 a simple ‘sequence of states’ has been outlined where the usual sequence of showing ‘red’, ‘orange’, and green is assumed. In certain types of cultures this is a typical everyday situation.

Thus we can assume a ‘state S1’ where the traffic light is showing ‘red’. This can be represented by the expression:

A

All participants know, that this expressions describes a real situation where the ‘learned meaning of this expression’ is in accordance with the actual ‘perceptions’ which are assumed to be in ‘accordance’ with some ‘real situation outside the brain and outside the body’. In that case the ‘speaker’ and ‘hearer’ of expression ‘A’ agree – under normal circumstances — that the ‘meaning’ associated with the expression ‘A’ is ‘true’. If the perception would provide ‘another concrete construct’ triggered by a traffic light showing ‘orange’ instead of ‘red’ then the learned meaning of expression ‘A’ would not match. In that mismatch situation speaker and hearer would agree – under normal circumstances — that the ‘meaning’ associated with the expression ‘A’ is ‘not true’, and this is a case of being classified as ‘false’.

Now, what could in such a situation be a ‘derivation’ in the context of a ‘natural logic’?

As has been mentioned before the ‘abstract structures’ of the meaning space are ‘dynamic constructions’ allocating many different properties of the perceived real world into ‘internal (neural = cognitive) clusters’ representing these properties within these structures. Thus, the abstract structure ‘traffic light’ is a structure possessing the typical collection of three different lights with their typical pattern of sequential activations.[19] A brain which has built up such abstract structures can use these to produce ‘forecasts’ by ‘reading its learned structures’!

Assume that the perceived situation is that state called S1 which can be described with the expression ‘A’:

S1 = {A}

From the learned abstract structure ‘traffic light’ the brain could ‘derive the rule’

R1:

IF there is a situation S which has a property described by an expressions ‘A’, THEN it can happen in a follow up state S’, that the expression ‘A’ does not any more match’, but expression ‘B’.

If we make the set of derivation rules X equal to the set comprising rule R1 with X = {R1} then we can built the following natural logic derivation:

S  ⊢X S’

with S ={A} and S’={B}.

This kind of derivation is radically different to a boolean logic derivation:

(i) While boolean logic can only derive something which is ‘already true’, natural logic can derive something which ‘could become true in the future’ by assuming, that the ‘learned meaning’ is ‘true’.

(ii) While boolean logic can only use derivation rules based on operations with expressions only, natural logic can exploit the vast amount of ‘learned meaning structures’ owned by an individual brain and which is partially ‘shared’ with other brains.

Based on (ii) a brain is always capable to ‘construct its own derivation rules’ simply by ‘exploiting’ its learned abstract (dynamical) structures. Thus every brain can ‘invent’ new types of logic only by using its ‘learned experience’.

From this follows directly that human actors which want to ‘think explicitly about some possible future’ should abandon boolean logic and instead should exercise to exploit their learned knowledge.

In a historical perspective it is very strange that the most advanced complex system of the whole known universe — the biosphere, and as part of it the homo sapiens population — decided to use as logic a system, which abandons all this fantastic inventions of more than 3.5 billion (10^9) years to select a system of sign operations, which is more than pure and of not too much help for survival. The construction of programmable machines (usually called computers) by using boolean logic has enabled an interesting tool, but only if we use this as ‘part of biological intelligence’.

— draft version —

Chapter

Everyday Language: English

eJournal: uffmm.org
ISSN 2567-6458, 19.August 2022 – 19 August 2022
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de

CONTEXT

This text is part of the subject COMMON SCIENCE as Sustainable Applied Empirical Theory, besides ENGINEERING, in a SOCIETY. It is a preliminary version, which is intended to become part of a book.

Everyday Language: English

In this section we repeat the everyday example from before, now with expressions from the English language. The situation is a human actor in front of a traffic light showing a ‘red’ light.

In this situation the human actor could say:

“The traffic light shows red.”

Some seconds (or minutes) later he would state:

“The traffic light shows orange.”

Again, after some seconds (or minutes) he would utter:

“The traffic light shows green.”

Then he would start to move away from the traffic light.

We could ‘name’ these expressions by abbreviation in the following way:

A := “The traffic light shows red.”

B := “The traffic light shows orange.”

C := “The traffic light shows green.”

After the introduction of these abbreviations this example looks completely as the example with the German expressions. And, indeed, it works completely similar. The reason for this is located in the ‘body system’ of a human actor with its special ‘brain’.

Figure: Simple outline of basic interactions between an empirical object with properties embedded in a situation and (human) actors with perception, meaning space, abstract structures functioning as cognitive models of possible real world somethings. An abstract structure usually includes more than one possible empirical situation thereby ‘transcending’ a perceptional ‘NOW’ into different possible (cognitive) states (encoding possible ‘future’ states). The internal meaning space with its manifold abstract structures allows lots of ‘logical derivations’ which are impossible looking only to utterances or to actual empirical settings.

n the following example we have a human actor being part of a traffic situation, who gives some fragments of a language description of what he is experiencing (in the next section this example will be given with the English language).

In a first situation the human actor would say:

“Die Ampel zeigt rot.”

Some seconds (or minutes) later he would state:

“Die Ampel zeigt orange.”

Again, after some seconds (or minutes) he would utter:

“Die Ampel zeigt grün.”

Then he would start to move away.

We could ‘name’ these expressions by abbreviation in the following way:

A := “Die Ampel zeigt rot.”

B := “Die Ampel zeigt orange.”

C := “Die Ampel zeigt grün.”

In the everyday situation where these statements will be uttered by a human actor this human actor would classify each statement as ‘being true’, because the ‘known meaning’ associated with these expressions is in that moment of being uttered in a ‘sufficient accordance’ with the perceived situation. Thus, one could classify the individual statements as ‘true’ while being ‘uttered’.

Using the abbreviations ‘A’, ‘B’, and ‘C’ we could apply the inference machinery of the boolean logic with

(1) A and B and C  ⊢X A or … B … or C

In the everyday situation where these statements have been uttered this logical inference would be wrong. If we would do it like in (1).

The reason for this insufficiency is grounded in the fact, that each statement from ‘A’, ‘B’, and ‘C’ is describing the property of a traffic light (being red, orange or green), and only one of these statements can be true at a certain point of time. Thus the ‘truth’ of these statements is ‘time dependent’! Furthermore works the traffic sign in an ‘action pattern’ which makes one ‘color’ ‘true’ and at the same time all other colors ‘false’. Thus a traffic light is a collection of statements like this:

(2) traffic light := {‘A and non B and non C’ or ‘non A and B and non C’ or ‘non A and non B and C’} (with ‘or’ as another boolean operator).

From this the following boolean derivations would be possible:

  • One of these statements can become true
  • If e.g. ‘A and non B and non C’ would become true, then one could derive that ‘A’ is true or ‘non B’ or ‘non C’. This would describe the case, where in the everyday world the red sign of the traffic light would be shining.

From the boolean derivation as such it would not be possible to decide, which of the possible variants would be the case in a certain moment. Because boolean logic in general has to assume a human actor (or any kind of actor with sufficient properties), who is able to associate the expressions with his internal meaning space, combined with the intention to classify which of the ‘logically possible variants’ is matching an ‘actual situation’, which offers those ‘meaning properties’, which are needed, to ‘make the expression an instance’ of this meaning case.

Naturally, it is a human actor who has to ‘invent’ the definition of a ‘traffic light’ in the format of (2), if he knows concrete examples of traffic lights in everyday situations. Because of this, because a human actor has an internal knowledge space with an internal meaning function μ, he ‘knows’ which kinds of properties are ‘related’ to that what is called a ‘traffic light’. And from this follows with ‘normal logic’ that

  1. If a traffic light shows a certain color, this is only valid in a certain time span (t,t’) and all the other colors of this traffic light are not active simultaneously.
  2. Thus uttering the statement ‘Die Ampel zeigt rot’ implies that this statement is true in that moment.
  3. By ‘normal logic’ every human actor — with the same meaning space — ‘knows implicitly’ that the other lights do not show their colors in that moment. To make the additional statements that ‘Die Ampel ist nicht gelb’ and ‘Die Ampel ist nicht grün’ are not necessary because every human actor would ‘derive’ these consequences ‘internally purely automatically’ (because our brains work in this fashion without explicitly asking whether they are allowed to do this).

— draft version —

Chapter

Predicate Logic

eJournal: uffmm.org
ISSN 2567-6458, 19.August 2022 – 19 August 2022
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de

CONTEXT

This text is part of the subject COMMON SCIENCE as Sustainable Applied Empirical Theory, besides ENGINEERING, in a SOCIETY. It is a preliminary version, which is intended to become part of a book.

Predicate Logic

Figure: Outline of the kind of expressions which are used for the ‘usual’ ‘Predicate Logic’. As one can see in history, many different variants are possible.

So-called ‘predicate logic’ can be found since the classical Greek philosophy (cf. [7], chapter 2), but in the ‘old times’ not in the format which we know and are using since Frege, Russel & Whitehead and others since the 20th century.

What one can observe in the talking about predicate logic is a constant reduction of the properties of predicate logic as well as the circumstances of usage. While we can find in the collection of texts associated with Aristotle called ‘Organon’ different dimensions beyond the pure expressions — in a not complete systematic way — do modern texts restrict themselves more or less to expressions only …. in theory, not in practice.

To discuss the topic of predicate logic in an everyday setting we will start with predicate logic from the point of view of expressions only and then we will try a look to the ‘conditions of usage’.

In the outline presented in figure 4 we take as a common assumption that human actors are the main actors producing and using predicate logic. From these human actors we know that they are ‘complex dynamic systems’ living in a complex dynamic environment (with the human actors as part of this environment making it even more complex than without human actors). Furthermore it is a historical fact that the homo sapiens population demonstrates since its beginning (before about 300.000 years somewhere in Africa) the special ability that their brains — embedded in their bodies — can organize a ‘communication by symbolic means’ in a way which enables these individual distributed brains to ‘coordinate’ the ‘behavior’ of their bodies in a growing complex manner. History shows how the ‘technology of communication’ has changed constantly beginning with written symbols, texts, libraries, data bases, connected data bases within computer networks called ‘cyberspace’.

Besides many thousands of ‘ordinary (= normal) languages’ the brains of the homo sapiens population have invented many ‘specialized languages’ extending the normal languages in many directions. Such a specialized language’ is completely depending from the given normal language. Without the used natural language a specialized language cannot exist; a specialized language as such is ‘nothing’; with a normal language as starting point a specialized language can allow quite complex ‘artificial symbolic structures’ which — used in an ‘adequate manner’ — can help the acting brains to ‘describe possible meanings’ which can eventually help to understand some parts of the ‘perceivable world outside the brain’ (and thereby some behavior of the brain itself!)

— draft version —