Category Archives: logic – formal

absolute truth, deductive logic, empirical basis, empirical theory, Karl Popper, logic, logic - formal, logical consequence, logical contradiction, objective knowledge, observation, Popper, pseudo science, subjective believe, truth

POPPER – Objective Knowledge (1971). Summary, Comments, how to develope further


eJournal: uffmm.org
ISSN 2567-6458, 07.March 22 – 12.March 2022, 10:55h
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de

BLOG-CONTEXT

This post is part of the Philosophy of Science theme which is part of the uffmm blog.

PREFACE

In this post a short summary of Poppers view of an empirical theory is outlined as he describes it in his article “Conjectural Knowledge: My Solution of the Problem of Induction” from 1971.[1] The view of Popper will be commented and the relationsship to the oksimo paradigm of the author will be outlined.

Empirical Theory according to Popper in a Nutshell

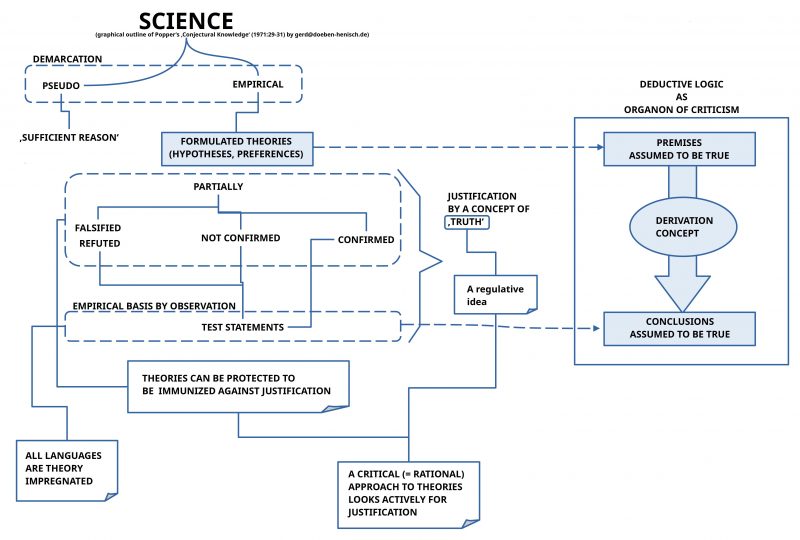
Figure: Popper’s concept from 1971 of an empirical theory, compressed in a nutshell. Graphic by Gerd Doeben-Henisch based on the article using Popper’s summarizing ideas on the pages 29-31

POPPER’S POSITION 1971

In this article from 1971 Popper discusses several positions. Finally he offers the following ‘demarcation’ between only two cases: ‘Pseudo Science’ and ‘Empirical Science’.(See p.29) In doing so this triggers the question how it is possible to declare something as an ‘objective empirical theory’ without claiming to have some ‘absolute truth’?

Although Popper denies to have some kind of absolute truth he will “not give up the search for truth”, which finally leads to a “true explanatory theory”.(cf. p.29) “Truth” plays the “role of a regulative idea”.(cf. p.30) Thus according to Popper one can “guess for truth” and some of the hypotheses “may well be true”.(cf.p.30)

In Popper’s view finally ‘observation’ shows up as that behaviour which enables the production of ‘statements’ as the ’empirical basis’ for all arguments.(cf.p.30) Empirical statements are a ‘function of the used language’.(cf. p.31)

This dimension of language leads Popper to the concept of ‘deductive logic’ which describes formal mechanisms to derive from a set of statements — which are assumed to be true — those statements, which are ‘true’ by logical deduction only. If statements are ‘logically false’ then this can be used to classify the set of assumed statements as ‘logically not consistent’. (cf. p.31)

comments on popper’s 1971-position 50 years later

The preceding outline of Popper’s position reveals a minimalist account of the ingredients of an ‘objective empirical theory’. But we as the readers of these ideas are living 50 years later. Our minds are shaped differently. The author of this text thinks that Popper is basically ‘true’, although there are some points in Popper’s argument, which deserve some comments.

Subjective – Absolute

Popper is moving between two boundaries: One boundary is the so called ‘subjective believe’ which can support any idea, and which thereby can include pure nonsense; the other boundary is ‘absolute truth’, which is requiring to hold all the time at all places although the ‘known world’ is evidently showing a steady change.

Empirical Basis

In searching for a possible position between these boundaries, which would allow a minimum of ‘rationality’, he is looking for an ’empirical Basis’ as a point of reference for a ‘rational theory’. He is locating such an empirical basis in ‘observation statements’ which can be used for ‘testing a theory’.

In his view a ‘rational empirical theory’ has to have a ‘set of statements’ (often called ‘assumptions’ of the theory or ‘axioms’) which are assumed to ‘describe the observable world’ in a way that these statements should be able to be ‘confirmed’ or be ‘falsified’.

Confirmation – Falsification

A ‘confirmation’ does not imply that the confirmed statement is ‘absolutely true’ (his basic conviction); but one can experience that a confirmed statement can function as a ‘hypothesis/ conjecture’ which ‘workes in the actual observation’. This does not exclude that it perhaps will not work in a future test. The pragmatical difference between ‘interesting conjectures’ and those which are of less interest is that a ‘repeated confirmation’ increases the ‘probability’, that such a confirmation can happen again. An ‘increasing probability’ can induce an ‘increased expectation’. Nevertheless, increased probabilities and associated increased expectations are no substitutes for ‘truth’.

A test which shows ‘no confirmation’ for a logically derived statement from the theory is difficult to interpret:

Case (i): A theory is claiming that a statement S refers to a proposition A to be ‘true in a certain experiment’, but in the real experiment the observation reveals a proposition B which translates to non-A which can interpreted as ‘the opposite to A is being the case’ (= being ‘true’). This outcome will be interpreted in the way that the proposition B interpreted as ‘non-A’ contradicts ‘A’ and this will be interpreted further in the way, that the statement S of the theory represents a partial contradiction to the observable world.

Case (ii): A theory is claiming that a statement S refers to a proposition A to be ‘true in a certain experiment’, but in the real experiment the observation reveals a proposition B ‘being the case’ (= being ‘true’) which shows a different proposition. And this outcome cannot be related to the proposition ‘A’ which is forecasted by the theory. If the statement ‘can not be interpreted sufficiently well’ then the situation is neither ‘true’ nor ‘false’; it is ‘undefined’.

Discussion: Case (ii) reveals that there exist an observable (empirical) fact which is not related to a certain ‘logically derived’ statement with proposition A. There can be many circumstances why the observation did not generate the ‘expected proposition A’. If one would assume that the observation is related to an ‘agreed process of generating an outcome M’, which can be ‘repeated at will’ from ‘everybody’, then the observed fact of a ‘proposition B distinguished from proposition A’ could be interpreted in the way, that the expectation of the theory cannot be reproduced with the agreed procedure M. This lets the question open, whether there could eventually exist another procedure M’ producing an outcome ‘A’. This case is for the actors which are running the procedure M with regard to the logically derived statement S talking about proposition A ‘unclear’, ‘not defined’, a ‘non-confirmation’. Otherwise it is at the same time no confirmation either.

Discussion: Case (i) seems — at a first glance — to be more ‘clear’ in its interpretation. Assuming here too that the observation is associated with an agreed procedure M producing the proposition B which can be interpreted as non-A (B = non-A). If everybody accepts this ‘classification’ of B as ‘non-A’, then by ‘purely logical reasons’ (depending from the assumed concept of logic !) ‘non-A’ contradicts ‘A’. But in the ‘real world’ with ‘real observations’ things are usually not as ‘clear-cut’ as a theory may assume. The observable outcome B of an agreed procedure M can show a broad spectrum of ‘similarities’ with proposition A varying between 100% and less. Even if one repeats the agreed procedure M several times it can show a ‘sequence of propositions <B1, B2, …, Bn>’ which all are not exactly 100% similar to proposition A. To speak in such a case (the normal case!), of a logical contradiction it is difficult if not impossible. The idea of Popper-1971 with a possible ‘falsification’ of a theory would then become difficult to interpret. A possible remedy for this situation could be to modify a theory in the way that a theory does forecast only statements with a proposition A which is represented as a ‘field of possible instances A = <a1, a2, …, am>’, where every ‘ai‘ represents some kind of a variation. In that modified case it would be ‘more probable’ to judge a non-confirmation between A as <a1, a2, …, am> and B as <B1, B2, …, Bn>, if one would take into account the ‘variability’ of a proposition.[3]

Having discussed the case of ‘non-confirmation’ in the described modified way this leads back again to the case of ‘confirmation’: The ‘fuzziness’ of observable facts even in the context of agreed procedures M of observation, which are repeatable by everyone (usually called measurement) requires for a broader concept of ‘similarity’ between ‘derived propositions’ and ‘observed propositions’. This is since long a hot debated point in the philosophy of science (see e.g. [4]). Until now does no general accepted solution exist for this problem.

Thus the clear idea of Popper to associate a theory candidate with a minimum of rationality by relating the theory in an agreed way to empirical observations becomes in the ‘dust of reality’ a difficult case. It is interesting that the ‘late Popper’ (1988-1991) has modified his view onto this subject a little bit more into the direction of the interpretation of observable events (cf. [5])

Logic as an Organon

In the discussion of the possible confirmation or falsification of a theory Popper uses two different perspectives: (i) in a more broader sense he is talking about the ‘process of justification’ of the theoretical statements with regard to an empirical basis relying on the ‘regulative idea of truth’, and (ii) in a more specialized sense he is talking about ‘deductive logic as an organon of criticism’. These two perspectives demand for more clarification.

While the meaning of the concept ‘theory’ is rather vague (statements, which have to be confirmed or falsified with respect to observational statements), the concept ‘deductive logic as an organon’ isn’t really clearer.

Until today we have two big paradigms of logic: (i) the ‘classical logic’ inspired by Aristotle (with many variants) and (ii) ‘modern formal logic’ (cf. [6]) in combination with modern mathematics (cf. [7],[8]). Both paradigms represent a whole universe of different variants, whose combinations into concrete formal empirical theories shows more than one paradigm.(cf. [4], [8], [10])

As outlined in the figure above the principal idea of logic in general follows the following schema: one has a set of expressions of some language L for which one assumes at least, that these expressions are classified as ‘true expressions’. According to an agreed procedure of ‘derivation’ one can derive (deduce, infer, …) other expressions of the language which are assumed to be classified as ‘true’ if the assumptions hold.[11]

The important point here is, that the modern concept of logic does not explain, what ‘true’ means nor exists there an explanation, how exactly a procedure looks like which enables the classification of an expression as ‘being true’. Logic works with the minimalist assumption that the ‘user of logic’ is using statements which he assumes to be ‘true’ independent of how this classification came into being. This frees the user of logic to deal with the cumbersome process of clarifying the meaning and the existence of something which makes a statement ‘true’, but on the other side the user of modern logic has no real control whether his ‘concept of derivation’ makes any sense in a real world, from which observation statements are generated claiming to be ’empirically true’, and that the relationships between these observational statements are appropriately ‘represented’ by the formal derivation concept. Until today there exists no ‘meta-theory’ which explains the relationship between the derivation concept of formal logic (there are many such concepts!) and the ‘dynamics of real events’.

Thus, if Popper mentions formal logic as a tool for the handling of assumed true statements of a theory, it is not really clear whether such a formal logical derivation really is appropriate to explain the ‘relationships between assumed true statements’ without knowing, which kind of reality is ‘designated’/ ‘referred to’ by such statements and their relationships between each other.

(Formalized) Theory and Logic

In his paper Popper does not explain too much what he is concretely mean with a (formalized) theory. Today there exist many different proposals of formalized theories for the usage as ’empirical theories’, but there is no commonly agreed final ‘template’ of a ‘formal empirical theory’.

Nevertheless we need some minimal conception to be able to discuss some of the properties of a theory more concretely. I will address this problem in another post accompanied with concrete applications.

COMMENTS

[1] Karl R.Popper, Conjectural Knowledge: My Solution of the Problem of Induction, in: [2], pp.1-31

[2] Karl R.Popper, Objective Knowledge. An Evolutionary Approach, Oxford University Press, London, 1972 (reprint with corrections 1973)

[3] In our everyday use of our ‘normal’ language it is the ‘normal’ case that a statement S like ‘There s a cup on the table’ can be interpreted in many different ways depending which concrete thing (= proposition B of the above examples) called a ‘cup’ or called ‘table’ can be observed.

[4] F. Suppe, Ed., The Structure of Scientific Theories, University of
Illinois Press, Urbana, 2nd edition, 1979.

[5] Gerd Doeben-Henisch, 2022,(SPÄTER) POPPER – WISSENSCHAFT – PHILOSOPHIE – OKSIMO-DISKURSRAUM, in: eJournal: Philosophie Jetzt – Menschenbild, ISSN 2365-5062, 22.-23.Februar 2022,
URL: https://www.cognitiveagent.org/2022/02/22/popper-wissenschaft-philosophie-oksimo-paradigma/

[6] William Kneale and Martha Kneale, The development of logic, Oxford University Press, Oxford, 1962 with several corrections and reprints 1986.

[7] Jean Dieudonnè, Geschichte der Mathematik 1700-1900, Friedrich Viehweg & Sohn, Braunschweig – Wiesbaden, 1985 (From the French edition “Abrégé d’histoire des mathématique 1700-1900, Hermann, Paris, 1978)

[8] Philip J.Davis & Reuben Hersh, The Mathematical Experience, Houghton Mifflin Company, Boston, 1981

[9] Nicolas Bourbaki, Elements of Mathematics. Theory of Sets, Springer-Verlag, Berlin, 1968

[10] Wolfgang Balzer, C.Ulises Moulines, Joseph D.Sneed, An Architectonic for Science. The Structuralist Program,D.Reidel Publ. Company, Dordrecht -Boston – Lancaster – Tokyo, 1987

[11] The usage of the terms ‘expression’, ‘proposition’, and ‘statement’ is in this text as follows: An ‘expression‘ is a string of signs from some alphabet A and which is accepted as ‘well formed expression’ of some language L. A ‘statement‘ is an utterance of some actor using expressions of the language L to talk ‘about’ some ‘experience’ — from the world of bodies or from his consciousness –, which is understood as the ‘meaning‘ of the statement. The relationship between the expressions of the statement and the meaning is located ‘in the actor’ and has been ‘learned’ by interactions with the world and himself. This hypothetical relationship is here called ‘meaning function  φ’. A ‘proposition‘ is (i) the inner construct of the meaning of a statement (here called ‘intended proposition’) and (ii) that part of the experience, which is correlated with the inner construct of the stated meaning (here called ‘occurring proposition’). The special relationship between the intended proposition and the occurring proposition is often expressed as ‘referring to’ or ‘designate’. A statement is called to ‘hold’/ to be ‘true’ or ‘being the case’ if there exists an occurring proposition which is ‘similar enough’ to the intended proposition of the statement. If such an occurring proposition is lacking then the designation of the statement is ‘undefined’ or ‘non confirming’ the expectation.

Follow-up Post

For a follow-up post see here.

empirical, empirical as existential, empirically sound, habit, inquiry, inquiry reformulated, limitations of logic, logic, logic - formal, logical consequence, logical derivation, logical inference, logical operators, logical subject-matter, operation of inquiry, operational, Postulational logic, process of inquiry, propositions, proximate-subject matter, rationality, ultimate subject-matter, valid propositions, warranted assertibility, warranted assertion

LOGIC. The Theory Of Inquiry (1938) by John Dewey – An oksimo Review – Part 3

eJournal: uffmm.org, ISSN 2567-6458, Aug 19-20, 2021
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de

SCOPE

In the uffmm review section the different papers and books are discussed from the point of view of the oksimo paradigm. [2] Here the author reads the book “Logic. The Theory Of Inquiry” by John Dewey, 1938. [1]

Part I – Chapter I

THE PROBLEM OF LOGICAL SUBJECT-MATTER

In this chapter Dewey tries to characterize the subject-matter of logic. From the year 1938 backwards one can look  into a long history of thoughts  with  at least 2500 years dealing in one or another sense with what has been called ‘logic’. His rough judgment is that the participants of the logic language  game  “proximate subject-matter of logic” seem to be widely in agreement what it is, but in the case of the  “ultimate subject-matter of logic” language game  there seem to exist different or even conflicting opinions.(cf. p.8)

Logic as a philosophic theory

Dewey illustrates the variety of views about the ultimate subject-matter of logic by citing several different positions.(cf. p.10) Having done this Dewey puts all these views together into a kind of a ‘meta-view’ stating that logic “is a branch of philosophic theory and therefore can express different philosophies.”(p.10) But  exercising  philosophy  ” itself must satisfy logical requirements.”(p.10)

And in general he thinks that  “any statement that logic is so-and-so, can … be offered only as a hypothesis and an indication of a position to be developed.”(p.11)

Thus we see here that Dewey declares the ultimate logical subject-matter grounded in some philosophical perspective which should be able “to order and account for what has been called the proximate subject-matter.”(p.11)  But the philosophical theory “must possess the property of verifiable existence in some domain, no matter how hypothetical it is in reference to the field in which it is proposed to apply it.”(p.11) This is an interesting point because this implies the question in which sense a philosophical foundation of logic can offer a verifiable existence.

Inquiry

Dewey gives some  hint for a possible answer by stating “that all logical forms …  arise within the operation of inquiry and are concerned with control of inquiry so that it may yield warranted assertions.”(p.11) While the inquiry as a process is  real, the emergence of logical forms has to be located in the different kinds of interactions between the researchers and some additional environment  in the process. Here should some verifiable reality be involved which is reflected in accompanying language expressions used by the researchers for communication.  This implies further that the used language expressions — which can even talk about other language expressions — are associated with propositions which can be shown to be valid.[4]

And  — with some interesting similarity with the modern concept of ‘diversity’ — he claims that in avoidance of any kind of dogmatism  “any hypothesis, no matter how unfamiliar, should have a fair chance and be judged by its results.”(p.12)

While Dewey is quite clear to use the concept of inquiry as a process leading to some results which are  depending from the starting point and the realized processes, he mentions additionally concepts like  ‘methods’, ‘norms’, ‘instrumentalities’, and  ‘procedures’, but these concepts are rather fuzzy. (cf. p.14f)

Warranted assertibility

Part of an inquiry are the individual actors which have psychological states like ‘doubt’ or ‘belief’ or  ‘understanding’ (knowledge).(p.15) But from these concepts follows nothing about needed  logical forms or rules.(cf.p.16f)  Instead Dewey repeats his requirement with the words “In scientific inquiry, the criterion of what is taken to be settled, or to be knowledge, is being so settled that it is available as a resource in further inquiry; not being settled in such a way as not to be subject to revision in further inquiry.”(p.17) And therefore, instead of using fuzzy concepts like (subjective) ‘doubt’, ‘believe’ or ‘knowledge’, prefers to use the concept “warranted assertibility”. This says not only, that you can assert something, but  that you can assert it also with ‘warranty’ based on the known process which has led to this result.(cf. p.10)

Introducing rationality

At this point the story takes a first ‘new turn’ because Dewey introduces now a first characterization of  the concept ‘rationality’ (which is for him synonymous with ‘reasonableness’). While the basic terms of the descriptions in an inquiry process are at least partially descriptive (empirical)  expressions, they are not completely “devoid of rational standing”.(cf. p.17) Furthermore the classification of final situations in an inquiry as ‘results’ which can be understood as ‘confirmations’ of initial  assumptions, questions or problems,  is only given in relations talking about the whole process and thereby they are talking about matters which are not rooted in  limited descriptive facts only. Or, as Dewey states it, “relations which exist between means (methods) employed and conclusions attained as their consequence.”(p.17) Therefore the following practical principle is valid: “It is reasonable to search for and select the means that will, with the maximum probability, yield the consequences which are intended.”(p.18)  And: “Hence,… the descriptive statement of methods that achieve progressively stable beliefs, or warranted assertibility, is also a rational statement in case the relation between them as means and assertibility as consequence is ascertained.”(p.18)

Suggested framework for ‘rationality’

Although Dewey does not exactly define the format of relations between selected means and successful consequences it seems ‘intuitively’ clear that the researchers have to have some ‘idea’ of such a relation which serves then as a new ‘ground for abstract meaning’ in their ‘thinking’. Within the oksimo paradigm [2] one could describe the problem at hand as follows:

  1. The researchers participating in an inquiry process have perceptions of the process.
  2. They have associated cognitive processing as well as language processing, where both are bi-directional mapped into each other, but not 1-to-1.
  3. They can describe the individual properties, objects, actors, actions etc. which are part of the process in a timely order.
  4. They can with their cognitive processing build more abstract concepts based on these primary concepts.
  5. They can encode these more abstract cognitive structures and processes in propositions (and expressions) which correspond to these more abstract cognitive entities.
  6. They can construct rule-like cognitive structures (within the oksimo paradigm  called ‘change rules‘) with corresponding propositions (and expressions).
  7. They can evaluate those change rules whether they describe ‘successful‘ consequences.
  8. Change rules with successful consequences can become building blocks for those rules, which can be used for inferences/ deductions.

Thus one can look to the formal aspect of formal relations which can be generated by an inference mechanism, but such a formal inference must not necessarily yield results which are empirically sound. Whether this will be the case is a job on its own dealing with the encoded meaning of the inferred expressions and the outcome of the inquiry.(cf. p.19,21)

Limitations of formal logic

From this follows that the concrete logical operators as part of the inference machinery have to be qualified by their role within the more general relation between goals, means and success. The standard operators of modern formal logic are only a few and they are designed for a domain where you have a meaning space  with only two objects: ‘being true’, being false’. In the real world of everyday experience we have a nearly infinite space of meanings. To describe this everyday large meaning space the standard logic of today is too limited. Normal language teaches us, how we can generate as many operators as we need  only by using normal language. Inferring operators directly from normal language is not only more powerful but at the same time much, much easier to apply.[2]

Inquiry process – re-formulated

Let us fix a first hypothesis here. The ideas of Dewey can be re-framed with the following assumptions:

  1. By doing an inquiry process with some problem  (question,…) at the start and proceeding with clearly defined actions, we can reach final states which either are classified as being a positive answer (success) of the problem of the beginning or not.
  2. If there exists a repeatable inquiry process with positive answers the whole process can be understood as a new ‘recipe’ (= complex operation, procedure, complex method, complex rule,law,  …) how to get positive answers for certain kinds of questions.
  3. If a recipe is available from preceding experiments one can use this recipe to ‘plan’ a new process to reach a certain ‘result’ (‘outcome’, ‘answer’, …).
  4. The amount of failures as part of the whole number of trials in applying a recipe can be used to get some measure for the probability and quality of the recipe.
  5. The description of a recipe needs a meta-level of ‘looking at’ the process. This meta-level description is sound (‘valid’) by the interaction with reality but as such the description  includes some abstraction which enables a minimal rationality.
Habit

At this point Dewey introduces another term ‘habit’ which is not really very clear and which not really does explain more, but — for whatever reason — he introduces such a term.(cf. p.21f)

The intuition behind the term ‘habit’ is that independent of the language dimension there exists the real process driven by real actors doing real actions. It is further — tacitly —  assumed that these real actors have some ‘internal processing’ which is ‘causing’ the observable actions. If these observable actions can be understood/ interpreted as an ‘inquiry process’ leading to some ‘positive answers’ then Dewey calls the underlying processes all together a ‘habit’: “Any habit is a way or manner of action, not a particular act or deed. “(p.20) If one observes such a real process one can describe it with language expressions; then it gets the format of a ‘rule’, a principle’ or a ‘law’.(cf. p.20)

If one would throw away the concept  ‘habit’, nothing would be missing. Whichever  internal processes are assumed, a description of these will be bound to its observability and will depend of some minimal  language mechanisms. These must be explained. Everything beyond these is not necessary to explain rational behavior.[5]

At the end of chapter I Dewey points to some additional aspects in the context of logic. One aspect is the progressive character of logic as discipline in the course of history.(cf. p.22)[6]

Operational

Another aspect is introduced by his statement “The subject-matter of logic is determined operationally.”(p.22) And he characterizes the meaning of the term ‘operational’ as representing the “conditions by which subject-matter is (1) rendered fit to serve as means and (2) actually functions as such means in effecting the objective transformation which is the end of the inquiry.”(p.22) Thus, again, the concept of inquiry is the general framework organizing means to get to a successful end. This inquiry has an empirical material (or ‘existential‘) basis which additionally can be described symbolically. The material basis can be characterized by parts of it called ‘means’ which are necessary to enable objective transformations leading to the end of the inquiry.(cf. p.22f)

One has to consider at this point that the fact of the existential (empirical) basis of every inquiry process should not mislead to the view that this can work without a symbolic dimension! Besides extremely simple processes every process needs for its coordination between different brains a symbolic communication which has to use certain expressions of a language. Thus   the cognitive concepts of the empirical  means and the followed rules can only get ‘fixed’ and made ‘clear’ with the usage of accompanying symbolic expressions.

Postulational logic

Another aspect mentioned by Dewey is given by the statement: “Logical forms are postulational.“(p.24) Embedded in the framework of an inquiry Dewey identifies requirements (demands, postulates, …) in the beginning of the inquiry which have to be fulfilled through the inquiry process. And Dewey sees such requirements as part of the inquiry process itself.(cf. p.24f) If during such an inquiry process some kinds of logical postulates will be used they have no right on their own independent of the real process! They can only be used as long as they are in agreement with the real process.  With the words of Dewey: “A postulate is thus neither arbitrary nor externally a priori. It is not the former because it issues from the relation of means to the end to be reached. It is not the latter, because it is not imposed upon inquiry from without, but is an acknowledgement of that to which the undertaking of inquiry commits us.”(p.26)  .

Logic naturalistic

Dewey comments further on the topic that “Logic is a naturalistic theory.“(p.27 In some sense this is trivial because humans are biological systems and therefore every process is a biological (natural) process, also logical thinking as part of it.

Logic is social

Dewey mentions further that “Logic is a social discipline.“(p.27) This follows from the fact that “man is naturally a being that lives in association with others in communities possessing language, and therefore enjoying a transmitted culture. Inquiry is a mode of activity that is socially conditioned and that has cultural consequences.”(p.27)  And therefore: “Any theory of logic has to take some stand on the question whether symbols are ready-made clothing for meanings that subsist independently, or whether they are necessary conditions for the existence of meanings —  in terms often used, whether language is the dress of ‘thought’ or is something without which ‘thought’ cannot be.” (27f) This can be put also in the following  general formula by Dewey: “…in every interaction that involves intelligent direction, the physical environment is part of a more inclusive social or cultural environment.” (p.28) The central means of culture is Language, which “is the medium in which culture exists and through which it is transmitted. Phenomena that are not recorded cannot be even discussed. Language is the record that perpetuates occurrences and renders them amenable to public consideration. On the other hand, ideas or meanings that exist only in symbols that are not communicable are fantastic beyond imagination”.(p.28)

Autonomous logic

The final aspect about logic which is mentioned by Dewey looks to the position which states that “Logic is autonomous“.(p.29) Although the position of the autonomy of logic — in various varieties — is very common in history, but Dewey argues against this position. The main point is — as already discussed before — that the open framework of an inquiry gives the main point of reference and logic must fit to this framework.[7]

SOME DISCUSSION

For a discussion of these ideas of Dewey see the next uocoming post.

COMMENTS

[1] John Dewey, Logic. The Theory Of Inquiry, New York, Henry Holt and Company, 1938  (see: https://archive.org/details/JohnDeweyLogicTheTheoryOfInquiry with several formats; I am using the kindle (= mobi) format: https://archive.org/download/JohnDeweyLogicTheTheoryOfInquiry/%5BJohn_Dewey%5D_Logic_-_The_Theory_of_Inquiry.mobi . This is for the direct work with a text very convenient.  Additionally I am using a free reader ‘foliate’ under ubuntu 20.04: https://github.com/johnfactotum/foliate/releases/).  The page numbers in the text of the review — like (p.13) — are the page numbers of the ebook as indicated in the ebook-reader foliate.(There exists no kindle-version for linux (although amazon couldn’t work without linux servers!))

[2] Gerd Doeben-Henisch, 2021, uffmm.org, THE OKSIMO PARADIGM
An Introduction (Version 2), https://www.uffmm.org/wp-content/uploads/2021/03/oksimo-v1-part1-v2.pdf

[3] The new oksimo paradigm does exactly this. See oksimo.org

[4] For the conceptual framework for the term ‘proposition’ see the preceding part 2, where the author describes the basic epistemological assumptions of the oksimo paradigm.

[5] Clearly it is possible and desirable to extend our knowledge about the internal processing of human persons. This is mainly the subject-matter of biology, brain research, and physiology. Other disciplines are close by like Psychology, ethology, linguistics, phonetics etc. The main problem with all these disciplines is that they are methodologically disconnected: a really integrated theory is not yet possible and not in existence. Examples of integrations like Neuro-Psychology are far from what  they should be.

[6] A very good overview about the development of logic can be found in the book The Development of Logic by William and Martha Kneale. First published 1962 with many successive corrected reprints by Clarendon Press, Oxford (and other cities.)

[7] Today we have the general problem that the concept of formal logic has developed the concept of logical inference in so many divergent directions that it is not a simple problem to evaluate all these different ‘kinds of logic’.

MEDIA

This is another unplugged recording dealing with the main idea of Dewey in chapter I: what is logic and how relates logic to a scientific inquiry.

Dewey, expressions, inference, inference concept, inference rule, logic, logic - formal, logical consequence, normal language, pragmatism, propositions, theory of inquiry, valid propositions

LOGIC. The Theory Of Inquiry (1938) by John Dewey – An oksimo Review – Part 1

eJournal: uffmm.org, ISSN 2567-6458, Aug 16 -Aug 18, 2021
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de

SCOPE

In the uffmm review section the different papers and books are discussed from the point of view of the oksimo paradigm. [2] Here the author reads the book “Logic. The Theory Of Inquiry” by John Dewey, 1938. [1]

PREFACE DEWEY 1938/9

If one looks to the time span between Dewey’s first published book  from 1887 (Psychology)  until 1938 (Logic) we have 51 years of experience.  Thus this book about logic can be seen as a book digesting a manifold knowledge from a very special point of view: from Logic as a theory of inquiry.

And because Dewey  is qualified as one of the “primary figures associated with the philosophy of pragmatism” [3] it is of no surprise that he in his preface to the book ‘Logic …’ [1] mentions not only as one interest the ” … interpretation of the forms and formal relations that constitute the standard material of logical tradition”(cf. p.1), but within this perspective he underlines the attention   particularly to  “…  the principle of the continuum of inquiry”(cf. p.1).

If one sees like Dewey the “basic conception of inquiry” as the “determination of an indeterminate situation” (cf. p.1)  then the implicit relations can enable  “a coherent account of the different propositional forms to be given”. This provides a theoretical interface to logical thinking as thinking in inferences as well as an philosophical interface to pragmatism as a kind of inquiry which sees strong relations between the triggering assumptions and the possible consequences created by agreed procedures leading from the given and expected to the final consequences.

Dewey himself is very skeptical about the term ‘Pragmatism’, because
“… the word lends itself [perhaps]  to misconception”, thus  “that it seemed advisable to avoid its use.” (cf. p.2) But Dewey does not stay with a simple avoidance;  he gives a “proper interpretation”  of the term ‘pragmatic’ in the way that “the function of consequences” can be interpreted as “necessary tests of the validity of propositions, provided these consequences are operationally instituted and are such as to resolve the specific problem evoking the operations.”(cf. p.2)

Thus Dewey assumes the following elements of a pragmatic minded process of inquiry:

  1. A pragmatic inquiry is a process leading to some consequences.
  2. These consequences can be seen as tests of the validity of propositions.
  3. As a necessary condition that a consequence can be qualified as a test of assumed propositions one has to assume  that “these consequences are operationally instituted and are such as to resolve the specific problem”.
  4. That consequences, which are different to the assumed propositions [represented by some expressions]  can be qualified as confirming an assumed validity of the assumed propositions, requires that the assumed validity can be represented as an expectation of possible outcomes which are observably decidable.

In other words: some researchers are assuming that some propositions represented by some expressions are valid, because they are convinced about this by their commonly shared observations of the propositions. They associate these assumed propositions with an expected outcome  represented by some expressions which can be interpreted by the researchers in a way, that they are able to decide whether an upcoming situation can be judged as that situation which is expected as a valid outcome (= consequence). Then there must exist some agreed procedures (operationally instituted) whose application to the given starting situation produces the expected outcome (=consequences). Then the whole process of a start situation with an given expectation as well as given procedures can generate a sequence of situations following one another with an expected outcome after finitely many situation.

If one interprets these agreed procedures as inference rules and the assumed expressions as assumptions and expectations then the whole figure can be embedded in the usual pattern of inferential logic, but with some strong extensions.

Dewey is quite optimistic about the conformity of this pragmatic view of an inquiry and a view of logic: “I am convinced that acceptance of the general principles set forth will enable a more complete and consistent set of symbolizations than now exists to be made.”(cf. p.2) But he points to one aspect, which would be necessary for a pragmatically  inspired view of logic which is in ‘normal logic’ not yet realized: “the need for development of a general theory of language in which form and matter are not separated.” This is a very strong point because the architecture of modern logic is fundamentally depending on the complete abandonment of meaning of language; the only remaining shadow of meaning resides in  the assumptions of the property of being ‘true’ or ‘false’ related to expressions (not propositions!). To re-introduce ‘meaning’ into logic by the usage of ‘normal language’ would be a complete rewriting of the whole of modern logic.

At the time of writing these lines by Dewey 1938 there was not the faintest idea in logic how such a rewriting of the whole logic could look like.

With the new oksimo paradigm there could perhaps exist a slight chance to do it. Why? Here are the main arguments:

  1. The oksimo paradigm assumes an inference process leading from some assumed starting situation to some consequences generated by the application of some agreed change-rules.
  2. All situations are assumed to have a twofold nature: (i) primarily they are given as expressions of some language (it can be a normal language!); (ii) secondarily these expressions are part of the used normal language, where every researches is assumed to have a ‘built-in’ meaning function which has during his/her individual learning collected enough ‘meaning’, which allows  a symbolically  enabled cooperation with other researchers.
  3. Every researcher can judge every time whether a given or inferred situation is in agreement with his interpretation of the expressions and their relation to the given or considered possible situation.
  4. If the researchers assume in the beginning additionally an expectation (goal/ vision) of a possible outcome (possible consequence), then it is possible at every point of the sequence to judge to which degree the actual situation corresponds to the expected situation.

The second requirement of Dewey for the usage of logic for a pragmatic inquiry was given in the statement  “that an adequate set of symbols depends upon prior institution of valid ideas of the conceptions and relations that are symbolized.”(cf. p.2)

Thus not only the usage of normal language is required but also some presupposed knowledge.  Within the oksimo paradigm it is possible to assume as much presupposed knowledge as needed.

RESULTS SO FAR

After reading the preface to the book it seems that the pragmatic view of inquiry combined with some  idea of modern logic can directly be realized within the oksimo paradigm.

The following posts will show whether this is a good working hypothesis or not.

COMMENTS

[1] John Dewey, Logic. The Theory Of Inquiry, New York, Henry Holt and Company, 1938  (see: https://archive.org/details/JohnDeweyLogicTheTheoryOfInquiry with several formats; I am using the kindle (= mobi) format: https://archive.org/download/JohnDeweyLogicTheTheoryOfInquiry/%5BJohn_Dewey%5D_Logic_-_The_Theory_of_Inquiry.mobi . This is for the direct work with a text very convenient.  Additionally I am using a free reader ‘foliate’ under ubuntu 20.04: https://github.com/johnfactotum/foliate/releases/). The page numbers in the text of the review — like (p.13) — are the page numbers of the ebook as indicated in the ebook-reader foliate.(There exists no kindle-version for linux (although amazon couldn’t work without linux servers!))

[2] Gerd Doeben-Henisch, 2021, uffmm.org, THE OKSIMO PARADIGM
An Introduction (Version 2), https://www.uffmm.org/wp-content/uploads/2021/03/oksimo-v1-part1-v2.pdf

[3] John Dewey, Wikipedia [EN]: https://en.wikipedia.org/wiki/John_Dewey

Continuation

See part 2 HERE.

MEDIA

Here some spontaneous recording of the author, talking ‘unplugged’ into a microphone how he would describe the content of the text above in a few words. It’s not perfect, but it’s ‘real’: we all are real persons not being perfect, but we have to fight for ‘truth’ and a better life while being ‘imperfect’ …. take it as ‘fun’ 🙂

axiom, empirical interpretation, empirical science, empirical theory, expert, expression [E], false, falsification, language, language - everyday L0, logic, logic - formal, logical consequence, logical contradiction, logical derivation, logical inference, meaning, meaning function, philosopher, Philosophy, Philosophy of Science, Popper, science, scientific theory, singular concept, singular statement, true, truth, universal concept, universal statement, verification

OKSIMO MEETS POPPER. Popper’s Position

eJournal: uffmm.org
ISSN 2567-6458, 31.March – 31.March  2021
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de

CONTEXT

This text is part of a philosophy of science  analysis of the case of the oksimo software (oksimo.com). A specification of the oksimo software from an engineering point of view can be found in four consecutive  posts dedicated to the HMI-Analysis for  this software.

POPPERs POSITION IN THE CHAPTERS 1-17

In my reading of the chapters 1-17 of Popper’s The Logic of Scientific Discovery [1] I see the following three main concepts which are interrelated: (i) the concept of a scientific theory, (ii) the point of view of a meta-theory about scientific theories, and (iii) possible empirical interpretations of scientific theories.

Scientific Theory

A scientific theory is according to Popper a collection of universal statements AX, accompanied by a concept of logical inference ⊢, which allows the deduction of a certain theorem t  if one makes  some additional concrete assumptions H.

Example: Theory T1 = <AX1,⊢>

AX1= {Birds can fly}

H1= {Peter is  a bird}

⊢: Peter can fly

Because  there exists a concrete object which is classified as a bird and this concrete bird with the name ‘Peter’ can  fly one can infer that the universal statement could be verified by this concrete bird. But the question remains open whether all observable concrete objects classifiable as birds can fly.

One could continue with observations of several hundreds of concrete birds but according to Popper this would not prove the theory T1 completely true. Such a procedure can only support a numerical universality understood as a conjunction of finitely many observations about concrete birds   like ‘Peter can fly’ & ‘Mary can fly’ & …. &’AH2 can fly’.(cf. p.62)

The only procedure which is applicable to a universal theory according to Popper is to falsify a theory by only one observation like ‘Doxy is a bird’ and ‘Doxy cannot fly’. Then one could construct the following inference:

AX1= {Birds can fly}

H2= {Doxy is  a bird, Doxy cannot fly}

⊢: ‘Doxy can fly’ & ~’Doxy can fly’

If a statement A can be inferred and simultaneously the negation ~A then this is called a logical contradiction:

{AX1, H2}  ⊢‘Doxy can fly’ & ~’Doxy can fly’

In this case the set {AX1, H2} is called inconsistent.

If a set of statements is classified as inconsistent then you can derive from this set everything. In this case you cannot any more distinguish between true or false statements.

Thus while the increase of the number of confirmed observations can only increase the trust in the axioms of a scientific theory T without enabling an absolute proof  a falsification of a theory T can destroy the ability  of this  theory to distinguish between true and false statements.

Another idea associated with this structure of a scientific theory is that the universal statements using universal concepts are strictly speaking speculative ideas which deserve some faith that these concepts will be provable every time one will try  it.(cf. p.33, 63)

Meta Theory, Logic of Scientific Discovery, Philosophy of Science

Talking about scientific theories has at least two aspects: scientific theories as objects and those who talk about these objects.

Those who talk about are usually Philosophers of Science which are only a special kind of Philosophers, e.g. a person  like Popper.

Reading the text of Popper one can identify the following elements which seem to be important to describe scientific theories in a more broader framework:

A scientific theory from a point of  view of Philosophy of Science represents a structure like the following one (minimal version):

MT=<S, A[μ], E, L, AX, ⊢, ET, E+, E-, true, false, contradiction, inconsistent>

In a shared empirical situation S there are some human actors A as experts producing expressions E of some language L.  Based on their built-in adaptive meaning function μ the human actors A can relate  properties of the situation S with expressions E of L.  Those expressions E which are considered to be observable and classified to be true are called true expressions E+, others are called false expressions  E-. Both sets of expressions are true subsets of E: E+ ⊂ E  and E- ⊂ E. Additionally the experts can define some special  set of expressions called axioms  AX which are universal statements which allow the logical derivation of expressions called theorems of the theory T  ET which are called logically true. If one combines the set of axioms AX with some set of empirically true expressions E+ as {AX, E+} then one can logically derive either  only expressions which are logically true and as well empirically true, or one can derive logically true expressions which are empirically true and empirically false at the same time, see the example from the paragraph before:

{AX1, H2}  ⊢‘Doxy can fly’ & ~’Doxy can fly’

Such a case of a logically derived contradiction A and ~A tells about the set of axioms AX unified with the empirical true expressions  that this unified set  confronted with the known true empirical expressions is becoming inconsistent: the axioms AX unified with true empirical expressions  can not  distinguish between true and false expressions.

Popper gives some general requirements for the axioms of a theory (cf. p.71):

  1. Axioms must be free from contradiction.
  2. The axioms  must be independent , i.e . they must not contain any axiom deducible from the remaining axioms.
  3. The axioms should be sufficient for the deduction of all statements belonging to the theory which is to be axiomatized.

While the requirements (1) and (2) are purely logical and can be proved directly is the requirement (3) different: to know whether the theory covers all statements which are intended by the experts as the subject area is presupposing that all aspects of an empirical environment are already know. In the case of true empirical theories this seems not to be plausible. Rather we have to assume an open process which generates some hypothetical universal expressions which ideally will not be falsified but if so, then the theory has to be adapted to the new insights.

Empirical Interpretation(s)

Popper assumes that the universal statements  of scientific theories   are linguistic representations, and this means  they are systems of signs or symbols. (cf. p.60) Expressions as such have no meaning.  Meaning comes into play only if the human actors are using their built-in meaning function and set up a coordinated meaning function which allows all participating experts to map properties of the empirical situation S into the used expressions as E+ (expressions classified as being actually true),  or E- (expressions classified as being actually false) or AX (expressions having an abstract meaning space which can become true or false depending from the activated meaning function).

Examples:

  1. Two human actors in a situation S agree about the  fact, that there is ‘something’ which  they classify as a ‘bird’. Thus someone could say ‘There is something which is a bird’ or ‘There is  some bird’ or ‘There is a bird’. If there are two somethings which are ‘understood’ as being a bird then they could say ‘There are two birds’ or ‘There is a blue bird’ (If the one has the color ‘blue’) and ‘There is a red bird’ or ‘There are two birds. The one is blue and the other is red’. This shows that human actors can relate their ‘concrete perceptions’ with more abstract  concepts and can map these concepts into expressions. According to Popper in this way ‘bottom-up’ only numerical universal concepts can be constructed. But logically there are only two cases: concrete (one) or abstract (more than one).  To say that there is a ‘something’ or to say there is a ‘bird’ establishes a general concept which is independent from the number of its possible instances.
  2. These concrete somethings each classified as a ‘bird’ can ‘move’ from one position to another by ‘walking’ or by ‘flying’. While ‘walking’ they are changing the position connected to the ‘ground’ while during ‘flying’ they ‘go up in the air’.  If a human actor throws a stone up in the air the stone will come back to the ground. A bird which is going up in the air can stay there and move around in the air for a long while. Thus ‘flying’ is different to ‘throwing something’ up in the air.
  3. The  expression ‘A bird can fly’ understood as an expression which can be connected to the daily experience of bird-objects moving around in the air can be empirically interpreted, but only if there exists such a mapping called meaning function. Without a meaning function the expression ‘A bird can fly’ has no meaning as such.
  4. To use other expressions like ‘X can fly’ or ‘A bird can Y’ or ‘Y(X)’  they have the same fate: without a meaning function they have no meaning, but associated with a meaning function they can be interpreted. For instance saying the the form of the expression ‘Y(X)’ shall be interpreted as ‘Predicate(Object)’ and that a possible ‘instance’ for a predicate could be ‘Can Fly’ and for an object ‘a bird’ then we could get ‘Can Fly(a Bird)’ translated as ‘The object ‘a Bird’ has the property ‘can fly” or shortly ‘A Bird can fly’. This usually would be used as a possible candidate for the daily meaning function which relates this expression to those somethings which can move up in the air.
Axioms and Empirical Interpretations

The basic idea with a system of axioms AX is — according to Popper —  that the axioms as universal expressions represent  a system of equations where  the  general terms   should be able to be substituted by certain values. The set of admissible values is different from the set of  inadmissible values. The relation between those values which can be substituted for the terms  is called satisfaction: the values satisfy the terms with regard to the relations! And Popper introduces the term ‘model‘ for that set of admissible terms which can satisfy the equations.(cf. p.72f)

But Popper has difficulties with an axiomatic system interpreted as a system of equations  since it cannot be refuted by the falsification of its consequences ; for these too must be analytic.(cf. p.73) His main problem with axioms is,  that “the concepts which are to be used in the axiomatic system should be universal names, which cannot be defined by empirical indications, pointing, etc . They can be defined if at all only explicitly, with the help of other universal names; otherwise they can only be left undefined. That some universal names should remain undefined is therefore quite unavoidable; and herein lies the difficulty…” (p.74)

On the other hand Popper knows that “…it is usually possible for the primitive concepts of an axiomatic system such as geometry to be correlated with, or interpreted by, the concepts of another system , e.g . physics …. In such cases it may be possible to define the fundamental concepts of the new system with the help of concepts which were originally used in some of the old systems .”(p.75)

But the translation of the expressions of one system (geometry) in the expressions of another system (physics) does not necessarily solve his problem of the non-empirical character of universal terms. Especially physics is using also universal or abstract terms which as such have no meaning. To verify or falsify physical theories one has to show how the abstract terms of physics can be related to observable matters which can be decided to be true or not.

Thus the argument goes back to the primary problem of Popper that universal names cannot not be directly be interpreted in an empirically decidable way.

As the preceding examples (1) – (4) do show for human actors it is no principal problem to relate any kind of abstract expressions to some concrete real matters. The solution to the problem is given by the fact that expressions E  of some language L never will be used in isolation! The usage of expressions is always connected to human actors using expressions as part of a language L which consists  together with the set of possible expressions E also with the built-in meaning function μ which can map expressions into internal structures IS which are related to perceptions of the surrounding empirical situation S. Although these internal structures are processed internally in highly complex manners and  are — as we know today — no 1-to-1 mappings of the surrounding empirical situation S, they are related to S and therefore every kind of expressions — even those with so-called abstract or universal concepts — can be mapped into something real if the human actors agree about such mappings!

Example:

Lets us have a look to another  example.

If we take the system of axioms AX as the following schema:  AX= {a+b=c}. This schema as such has no clear meaning. But if the experts interpret it as an operation ‘+’ with some arguments as part of a math theory then one can construct a simple (partial) model m  as follows: m={<1,2,3>, <2,3,5>}. The values are again given as  a set of symbols which as such must not ave a meaning but in common usage they will be interpreted as sets of numbers   which can satisfy the general concept of the equation.  In this secondary interpretation m is becoming  a logically true (partial) model for the axiom Ax, whose empirical meaning is still unclear.

It is conceivable that one is using this formalism to describe empirical facts like the description of a group of humans collecting some objects. Different people are bringing  objects; the individual contributions will be  reported on a sheet of paper and at the same time they put their objects in some box. Sometimes someone is looking to the box and he will count the objects of the box. If it has been noted that A brought 1 egg and B brought 2 eggs then there should according to the theory be 3 eggs in the box. But perhaps only 2 could be found. Then there would be a difference between the logically derived forecast of the theory 1+2 = 3  and the empirically measured value 1+2 = 2. If one would  define all examples of measurement a+b=c’ as contradiction in that case where we assume a+b=c as theoretically given and c’ ≠ c, then we would have with  ‘1+2 = 3′ & ~’1+2 = 3’ a logically derived contradiction which leads to the inconsistency of the assumed system. But in reality the usual reaction of the counting person would not be to declare the system inconsistent but rather to suggest that some unknown actor has taken against the agreed rules one egg from the box. To prove his suggestion he had to find this unknown actor and to show that he has taken the egg … perhaps not a simple task … But what will the next authority do: will the authority belief  the suggestion of the counting person or will the authority blame the counter that eventually he himself has taken the missing egg? But would this make sense? Why should the counter write the notes how many eggs have been delivered to make a difference visible? …

Thus to interpret some abstract expression with regard to some observable reality is not a principal problem, but it can eventually be unsolvable by purely practical reasons, leaving questions of empirical soundness open.

SOURCES

[1] Karl Popper, The Logic of Scientific Discovery, First published 1935 in German as Logik der Forschung, then 1959 in English by  Basic Books, New York (more editions have been published  later; I am using the eBook version of Routledge (2002))

 

 

knowledge about the world, logic, logic - formal, meaning function, set, set theory, vision

THE OKSIMO CASE as SUBJECT FOR PHILOSOPHY OF SCIENCE. Part 3. Generate a Vision

eJournal: uffmm.org
ISSN 2567-6458, 23.March – 24.March 2021
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de

CONTEXT

This text is part of a philosophy of science  analysis of the case of the oksimo software (oksimo.com). A specification of the oksimo software from an engineering point of view can be found in four consecutive  posts dedicated to the HMI-Analysis for  this software.

GENERATE A VISION

As explained in the preceding post a basic idea of the oksimo behavior space is to bring together different human actors, let them share their knowledge and experience of some real part of their world and then they are invited to  think about, how one can   improve this part.

In this text we will deal with this improvement of a given situation S. It is assumed here that any kind of improvement needs some idea, a vision [V] of a  possible real situation Sfut, which is not yet real but which in principal could become real. The vision of a possible real situation can in the beginning only exist as a set of Expressions ES whose  meaning is accessible by the meaning function φ applied to the expression ES as φ(ES) = Sfut = V. The vision V exists therefore as intended meaning only. An intended but not yet real meaning appears to us as as an idea in our mind,  which we can share  with other human actors by expressions classified as visions.

Such an intended future situation Sfut, the vision V, can be said to be real or true if there will be a point in  time in the future where Sfut   exists as a given  real situation S about which  can be said that S is fitting as an instance the meaning of the set of expressions ES describing the   situation S.

Le us for instance assume as a given real situation the  situation S with the describing expression ES= {There is a white wooden table}.

Le us for instance assume as a vision V  the describing expression EV = {There is a black metallic  table}.

The expression EV alone gives no hints whether it is describing a real situation or an intended possible future situation. This can only be decided based on actual knowledge about the world KRW which enables a human actor to  classify  a situation S either as actual given or as not actual given but generally possible. Depending on such a classification of a human actor A the human actor can decide whether the expression ES= {There is a white wooden table} is decidable as true or the expression EV = {There is a black metallic  table}. As long as the situation S is given as a real situation which corresponds to the expression ES= {There is a white wooden table} then the other expression EV = {There is a black metallic  table}  can be classified as not yet given.

FORMAL LOGIC BEYOND MEANING

(Last change: March 24, 2021)

Until now it has been stressed that expressions of a language L — external as well as internal – can only be understood   in connection with the assumed built-in meaning function φ which enables a mapping inside a brain between different kinds of brain   states  NN and a subset of these brain states  Lint  which is  representing the expressions of an inner  language, Lint ⊆ NN.

Assuming this we can look  to given sets of external expressions like  E and E’ of the external language L nevertheless in a purely formal way. Let us assume for instance the following two sets:

ES = {There is a table. The table is white. The table is quadratic.}

EV = {There is a table. The table is black. The table is round. The table allows four seats.}

If we look to both sets purely formally from the point of set theory then we can  apply set operations like the following ones:

  1. Cardinality of the sets (amount of members): |ES| = 3,  |EV| = 4
  2. Intersection (what is common to both): ES ∩ EV = {There is a table}
  3. Cardinality of the intersection: |{There is a table}| = 1
  4. Degree of sharing of EV to ES  as percentage = 1/4 = 25%

Thus purely formally without looking to the presupposed meaning we can say that the set EV representing the vision does  25% of its content share with the set ES representing the actual given real situation S.

If by some reason the actual situation S would change and thereby the corresponding set of expressions ES would change one can repeat the set operations and thereby one can monitor the relationship of the  given actual situation S and the vision V. If for instance a young couple wants to by a new table according to the vision EV owing actual a table according to the description ES than it can happen that the young couple  will find different kinds of tables t1, t2, …, tn  in  the furniture shops. The degree of similarity between the wanted table according to the vision V and the found tables ti in the furniture shops can vary between at least 25% and 100%. After 6 hours of looking around with the result that the best candidate ti reached  only 75% it is conceivable that the young couple changes their goal from 100% fulfillment to only 75%, or not. She says: “No, I want 100%”.

MEANING IN THE BACKGROUND

What one can see here is that formal mechanisms can work with sets of expressions without looking to the actual meaning. But it is at the same time clear that these formal operations are only useful seen in a  bigger framework where these expressions are clearly rooted in the meaning spaces of  every human actor participating in a communication inside a group of human actors — experts, citizens, people … –, where the group wants to clarify the relation between an actual given situation S and another not yet given situation Sfut which appears to the group as a vision of a possible situation which — by reasons only known to this group — seems to be more favorable.