eJournal: uffmm.org
ISSN 2567-6458, 19.August 2022 – 19 August 2022
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de

CONTEXT

This text is part of the subject COMMON SCIENCE as Sustainable Applied Empirical Theory, besides ENGINEERING, in a SOCIETY. It is a preliminary version, which is intended to become part of a book.

Boolean Logic

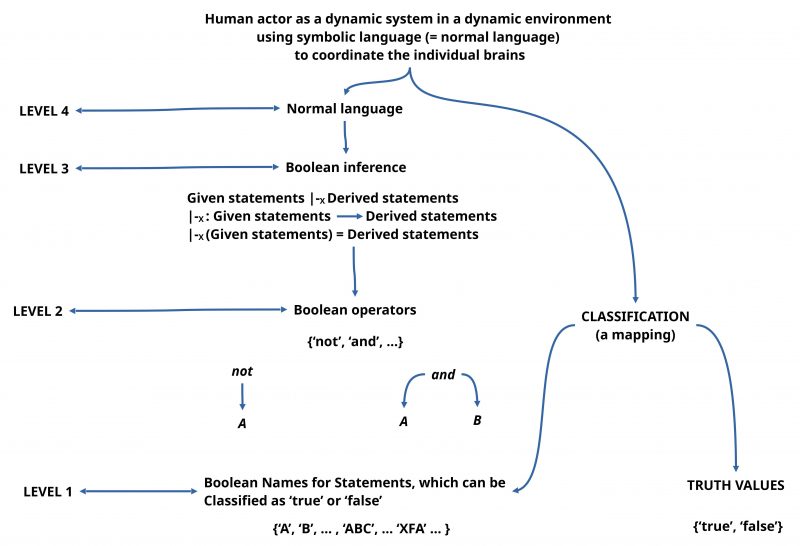
In the language of boolean logic — also called ‘propositional logic’ (but see [17]) — we have only expressions for ‘names’ of statements — like ‘A’, ‘B’, ‘CD’, … — , which can be classified (on a meta-level!) as being ‘true‘ or ‘false‘.

Whether one of the used names for statements is ‘true’ or ‘false’ has to be explained ‘separately’ — on a meta-level! — often written in a list or table called ‘truth table’ like:

1. A, true
2. B, false
3. C, false

Further we have some expressions naming ‘logical operators’ which we write here as ‘not‘ and ‘and‘. Strictly speaking these are on a ‘meta-level’ compared to the expressions representing statements which can be true or false.

Thus we could write the compound statement ‘A and B and C’

claiming that the whole expression has the meta-property of being true independent which truth values the individual statement expressions B’ and ‘C’ are assumed to have.

This simultaneous occurrence of two different meta-levels in the description of boolean logic expressions raises the question, how these metal-levels are ‘interacting’? The discussion of this question will be postponed here until we have discussed what is called a ‘logical derivation’.

A ‘logical derivation rule’ tells us that if we have an expression like ‘A and B’ ‘assumed’ to be ‘true’ than we can ‘derive’ from this expression that the expression ‘A’ or ‘B’ alone is also ‘true’. Thus with our introductory example, that the expression A and B and C is assumed to be true, we could ‘logically derive’ that the expressions A, or B, or C taken ‘alone’ are true either. In the logical meta-language we could describe this derivation relation as

A and B and C  ⊢_X A

or

A and B and C  ⊢_X B

or

A and B and C  ⊢_X C

where the sign ⊢_X denotes the logical derivation operator (meta-level !) with the arguments (left side) A and B and C and (right side) A or B or C. The index sign ‘X’ represents the set of derivation rules. In this case we have only one rule, therefore X = {if we have an expression like ‘A and B’ ‘assumed’ to be ‘true’, than we can ‘derive’ from this expression that the expression ‘A’ or ‘B’ alone is also ‘true’}

Coming back to the question of the interplay between the meta-level assumption that the expression C is assumed to be false but can be derived from the compound statement A and B and C as being ‘true’ reveals that the property of being ‘false’ of an individual statement and the property of an individual statement ‘C’ to be in a logical derivation ‘true’ describes apparently two different properties.

A possible solution of this meta-problem can be to introduce the convention, that the ‘individual true-false qualification’ can be expressed by ‘C’ as encoding ‘C is true individually’ and ‘not C’ as encoding ‘C is false individually’. But this ‘convention’ will only work if it would be ‘done’ before’ a logical derivation (again a meta-level matter). Thus, if one assumes the individual true-false qualifications of the before mentioned truth-table as ‘given’, than we had to write the compound statement as

A and not B and not C

which could yield the following derivations

A and not B and not C  ⊢_X A

or

A and not B and not C  ⊢_X not B

or

A and not B and not C ⊢_X not C

Thus we have presupposed ‘individual truth values’ and then one can logically derive either ‘B’ or ‘not B’ as ‘logically true’.

This discussion of ‘individual truth values’ compared to ‘logically derived truth values’ raises confusion. Indeed, boolean logic as such takes only names for expressions like ‘A’ or ‘B’ as arguments for their logical operators — ‘not’, ‘and’, … — being fed into a logical derivation relation — ⊢_X — without taking into account individual truth values. This part is ‘delegated’ to the user of boolean logic; the possible ‘interpretation’ of boolean logic expressions’ with ‘real truth’ is ‘outside of boolean logic’!

The leading idea is therefore that the usage of a symbolic language has to be understood as an interaction of several ‘levels of meaning’ simultaneously. One single language expression can be seen from the perspective of ‘meaning’ (the adaptive built function in every human actor) as having several ‘levels of meaning’. In the case of boolean logic this are at least four levels.

More aspects of the case of boolean logic will be discussed in the following sections.

— draft version —