eJournal: uffmm.org
ISSN 2567-6458, 19.August 2022 – 19 August 2022
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de
CONTEXT
This text is part of the subject COMMON SCIENCE as Sustainable Applied Empirical Theory, besides ENGINEERING, in a SOCIETY. It is a preliminary version, which is intended to become part of a book.
Everyday Language: English
In this section we repeat the everyday example from before, now with expressions from the English language. The situation is a human actor in front of a traffic light showing a ‘red’ light.
In this situation the human actor could say:
“The traffic light shows red.”
Some seconds (or minutes) later he would state:
“The traffic light shows orange.”
Again, after some seconds (or minutes) he would utter:
“The traffic light shows green.”
Then he would start to move away from the traffic light.
We could ‘name’ these expressions by abbreviation in the following way:
A := “The traffic light shows red.”
B := “The traffic light shows orange.”
C := “The traffic light shows green.”
After the introduction of these abbreviations this example looks completely as the example with the German expressions. And, indeed, it works completely similar. The reason for this is located in the ‘body system’ of a human actor with its special ‘brain’.
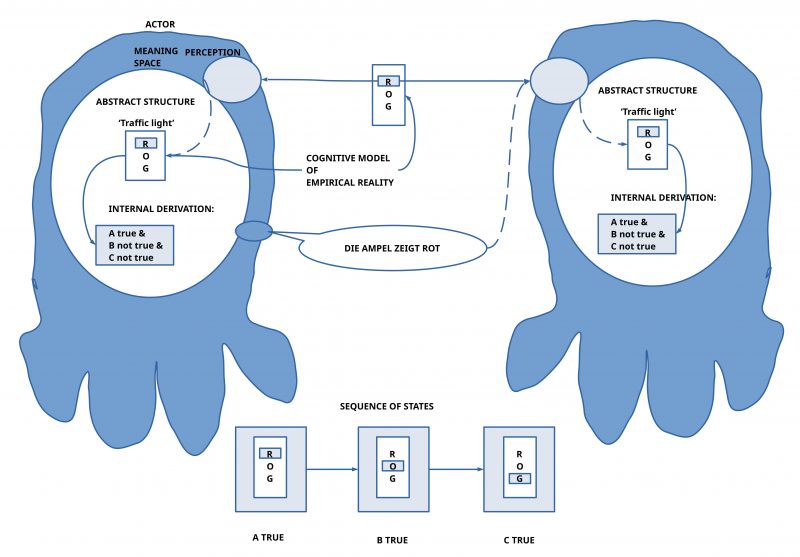
n the following example we have a human actor being part of a traffic situation, who gives some fragments of a language description of what he is experiencing (in the next section this example will be given with the English language).
In a first situation the human actor would say:
“Die Ampel zeigt rot.”
Some seconds (or minutes) later he would state:
“Die Ampel zeigt orange.”
Again, after some seconds (or minutes) he would utter:
“Die Ampel zeigt grün.”
Then he would start to move away.
We could ‘name’ these expressions by abbreviation in the following way:
A := “Die Ampel zeigt rot.”
B := “Die Ampel zeigt orange.”
C := “Die Ampel zeigt grün.”
In the everyday situation where these statements will be uttered by a human actor this human actor would classify each statement as ‘being true’, because the ‘known meaning’ associated with these expressions is in that moment of being uttered in a ‘sufficient accordance’ with the perceived situation. Thus, one could classify the individual statements as ‘true’ while being ‘uttered’.
Using the abbreviations ‘A’, ‘B’, and ‘C’ we could apply the inference machinery of the boolean logic with
(1) A and B and C ⊢X A or … B … or C
In the everyday situation where these statements have been uttered this logical inference would be wrong. If we would do it like in (1).
The reason for this insufficiency is grounded in the fact, that each statement from ‘A’, ‘B’, and ‘C’ is describing the property of a traffic light (being red, orange or green), and only one of these statements can be true at a certain point of time. Thus the ‘truth’ of these statements is ‘time dependent’! Furthermore works the traffic sign in an ‘action pattern’ which makes one ‘color’ ‘true’ and at the same time all other colors ‘false’. Thus a traffic light is a collection of statements like this:
(2) traffic light := {‘A and non B and non C’ or ‘non A and B and non C’ or ‘non A and non B and C’} (with ‘or’ as another boolean operator).
From this the following boolean derivations would be possible:
- One of these statements can become true
- If e.g. ‘A and non B and non C’ would become true, then one could derive that ‘A’ is true or ‘non B’ or ‘non C’. This would describe the case, where in the everyday world the red sign of the traffic light would be shining.
From the boolean derivation as such it would not be possible to decide, which of the possible variants would be the case in a certain moment. Because boolean logic in general has to assume a human actor (or any kind of actor with sufficient properties), who is able to associate the expressions with his internal meaning space, combined with the intention to classify which of the ‘logically possible variants’ is matching an ‘actual situation’, which offers those ‘meaning properties’, which are needed, to ‘make the expression an instance’ of this meaning case.
Naturally, it is a human actor who has to ‘invent’ the definition of a ‘traffic light’ in the format of (2), if he knows concrete examples of traffic lights in everyday situations. Because of this, because a human actor has an internal knowledge space with an internal meaning function μ, he ‘knows’ which kinds of properties are ‘related’ to that what is called a ‘traffic light’. And from this follows with ‘normal logic’ that
- If a traffic light shows a certain color, this is only valid in a certain time span (t,t’) and all the other colors of this traffic light are not active simultaneously.
- Thus uttering the statement ‘Die Ampel zeigt rot’ implies that this statement is true in that moment.
- By ‘normal logic’ every human actor — with the same meaning space — ‘knows implicitly’ that the other lights do not show their colors in that moment. To make the additional statements that ‘Die Ampel ist nicht gelb’ and ‘Die Ampel ist nicht grün’ are not necessary because every human actor would ‘derive’ these consequences ‘internally purely automatically’ (because our brains work in this fashion without explicitly asking whether they are allowed to do this).
— draft version —
