eJournal: uffmm.org, ISSN 2567-6458,
22.August 2022 – 24.August 2022, 17:30h
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de
SCOPE
In the uffmm review section the different papers and books are discussed from the point of view of the oksimo paradigm, which is embedded in the general view of a generalized ‘citizen science’ as a ‘computer aided sustainable applied empirical theory’ (CSAET). In the following text the author will discuss parts of the book “Structural Stability and Morphogenesis: An Outline of a General Theory of Models” from René Thom, originally as a French edition 1972, after several new editions updated in 1988 by the author and translated by H.D.Fowler 1988 into English, published 1989.
CONTEXT
In the foundational post with the title “COMMON SCIENCE as Sustainable Applied Empirical Theory, besides ENGINEERING, in a SOCIETY” a central idea is that a sustainable society has besides the challenge of the right usage of resources the other big challenge related to the ‘cognitive dimension’ as medium of its coordinated actions addressing a sufficiently well prepared planet for the survival of the biosphere in the future. Part of the cognitive dimension is the ability to ‘predict’ a — hopefully — ‘optimal’ course of events leading into the future as a guideline for the life today. It appears to the author of this review that the book of René Thom can give some ‘advice’ for a deeper understanding of the nature of ‘prediction’ using ideas of mathematics, especially ‘topology’ and ‘catastrophe theory’.
Mapping Nature into Formal Models
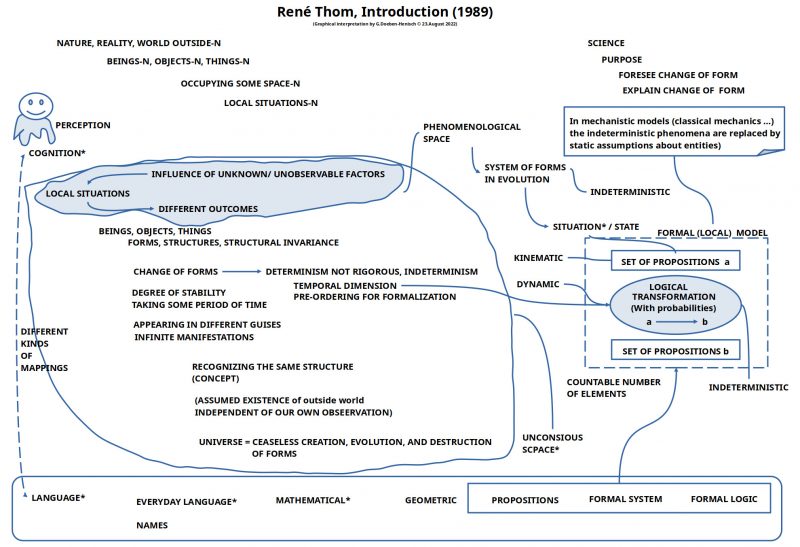
the big picture first
There are multiple ways to approach the ideas of René Thom in his introduction. Let us try an approach coming from the ‘outside’ and then ‘digging into the hidden structures’.
The outside framework is characterized by nature, the ‘real world outside’, by human actors occurring in this world with their bodies, and ‘language communication’ between human actors.
With regard to ‘language’ Thom cites many different ‘variants of language’ besides the ‘everyday language’ like ‘formal logic’, ‘formal systems’, ‘propositions’ etc., but he does not give a systematic account of these different variants; he does not explain the systematic relationships between these different variants.
The inward interaction between the real world outside and a human actor is characterized by ‘perception’. Perception maps properties of the outside world into the inner states of the body, especially into the brain, but Thom never mentions the brain explicitly. These mapped properties from the outside world inside the body are circumscribed for instance as ‘local situations’, ‘beings, objects, things’, ‘change of forms’, ‘degree of stability’, ‘different guises’. But because Thom doesn’t offer some explicit conceptual framework of the ‘inner space’ of a human actor, these concepts have no clear meaning. They only ‘trigger’ in the reader some associations in his everyday language understanding of some possible related meanings without a clear context.
Thom’s remark of a ‘phenomenological space’ remains a bit ‘cryptic’. In science it is common to associate the ‘phenomenological space’ with the way how the ‘world outside’ ‘appears to us’, but — using philosophical reasoning enhanced by brain science and experimental psychology — the properties of the outside world ‘as such’ are not available for the brain in the body. Only the ‘transformation’ of the outside world properties to the different perceptional organs of the body and their processing during ‘perception’ — thereby interacting at least with the memory — enables some ‘neuronal signals’ which are the ‘base ground’ for our brain to ‘compute’ some structures which we are using as ‘phenomena’ in our ‘conscious thinking’. Thus from the point of view of modern philosophy the ‘phenomenal space’ appears to be a space ‘inside the brain’, and this space is accompanied by the ‘unconscious space of cognition’, who is doing the ‘real job’; the ‘phenomenal space’ seems — today — to be a function of this unconscious cognitive space.
Despite the ‘vagueness’ of the descriptive wordings so far Thom introduces more concepts of the ‘inner world’, which seem to be intended as to differentiate the other words a little bit more.
Thus, the ‘infinite manifestations’ of the ‘appearing different guises’ of things can be ‘recognized as the same structure’, or that we ‘assume the existence of the outside world’ ‘independent of our own observation’.
With regard to ‘local situations’ which we can recognize, he reflects about the possible ‘influence of unknown/ unobservable factors’ which can cause ‘different outcomes’, that means different changes in the local situations.
More generally he thinks about the ‘universe’ as a ‘ceaseless creation’, which manifests itself in an ‘evolution’, which is accompanied by a ‘destruction of forms’. The destruction of forms is the same as the ‘change of forms’, which Thom classifies as ‘not rigorous deterministic’, hence ‘indeterministic’. The other aspect of ongoing changes is a ‘temporal dimension’ showing up; translated in a certain kind of ‘ordering’ these changes can be ‘translated’ into a formalization as a succession of states. Each state will be represented by a ‘set of properties’. With the aid of some logical inference mechanism it is possible to ‘transform’ one set of properties into another set of properties, including a measure for the probability, that the next set of properties will be inferred.
While the real world as such appears to us as some infinite source of phenomena with an unknown number of hidden factors are the elements of the outside world in general somehow infinite and indeterministic in their occurrence. But a human actor looking into this phenomenal space he can decide to assume the open character of phenomena as being describable as clear-cut finite things — as in ‘classical mechanics’ –, which allows a ‘deterministic’ handling of the phenomena. With other conceptual strategies — like in ‘quantum mechanics’ — the primary phenomena are classified as ‘indeterministic by nature’ which translates into logical inferences which are also ‘indeterministic’.
The overall purpose of science sees Thom as given in the intention to ‘foresee change of form’ and to ‘explain change of form’.
observables – local models – ultimate natuRe of reality
Thom points out that finally for a ‘macroscopic description of a system’ only the ‘observables’ of a local system are available.(cf. p.6f) What is ‘behind’ these observables, what exactly has to be understood by the ‘ultimate nature of reality’, this cannot completely be covered by a local system, by no local system.(cf. p.6f) Whether all local systems can finally be integrated into one coherent global system is an open question.(p.7)
a mathematics of discontinuities?
Thom considers further the fact that in common everyday experience we encounter many phenomena which appear in themselves to be very trivial but which are opposing a simple mathematical description.(cf. p.9) The main characteristic of these everyday phenomena is ‘discontinuity’. Because all applicable quantitative mathematical models rely on ‘continuity’ and ‘continuous functions’ this reduces the probability that science starts to describe ‘discontinuity’.(cf. p.9) Nevertheless there are more and more disciplines which are confronted with ‘discontinuous’ phenomena, which are ‘unstable’, show nearly ‘no repetition’ and do not fit easily in a mathematical model.(cf. p.9)
Thom gives a short outline of an idea how to cope with discontinuity by constructing a model of a set M of ‘observables’ which as such are ‘stable’, but they include a closed subset K of ‘catastrophes’ which manifest themselves as ‘singularities’ provoking a ‘discontinuity’ which can cause a ‘change’ on the observables, which constitutes the global phenomenon of ‘morphogenesis’.(cf. p.7) By not knowing in advance the ‘dynamics’ X underlying these changes it is possible to ‘reconstruct’ (step-wise) the underlying dynamics X by observing the global morphogenesis by recurring to the local changes too.(cf. p.7)
Thom underlines that it is not the local singularity as such which manifests the underlying dynamics X but the ‘accumulation’ of all singularities into ‘one global phenomenon’, which has to be explained.(cf. p.8) And because the ‘statistics’ of the local changes, which can be correlated with the local accidents, is determined by the underlying dynamics, it will not suffice to rely only on a local change; all changes together have to be explained. This can imply more than three dimensions of an euclidean space.(cf. p.8)
Discussion of Thom’s Position
There are some aspects which could be discussed in front of Thom’s position.
One major point could be his ‘vagueness’ with regard to the inner structure and processing of a human actor. Since 1972 (1989) many new deep insights have been revealed by disciplines like brain sciences in connection with experimental psychology and biology. I will not discuss this point here. There are several posts in the uffmm.org blog which are dealing with these topics.
What catches the attention of the reviewer here is the position of Thom considering the phenomenon of ‘discontinuities’ (changes) which not as a ‘single change’ represent a phenomenon but as a ‘series of changes’ which can not be classified as a ‘classical quantitative continuous’ phenomenon.
He thinks that especially ‘topological thinking’ can be of help here.
Comparing Thom’s position with the position of the the concept of a ‘sustainable empirical theory’ as it is outlined in the uffmm.org blog, especially condensed as a ‘theory producing process’ called ‘oksimo-R process paradigm’, it seems to be not only possible to solve the problem without topology, but — perhaps — even better without topology.
This results from the fact that the oksimo-R process paradigm presupposes a conceptual framework where not only the human actor as ‘theory producer’ is assumed to be located with his body in a ‘body-external empirical world’, but there exist also some additional assumptions about the ‘internal structure’ and the ‘internal processing’ of human actors, which are ‘explaining’ to a certain degree how a human actor can process properties of his environment — including his own body — within a cognitive and emotional space as well how he can ‘map’ parts of these spaces into sets of expressions of his everyday language. Based on such a ‘process model’ of a human actor it is possible to ‘explain’ additionally the language-based communication between different human actors whereby the different brains in the bodies can share some knowledge and emotions and can coordinate their actions.
The concept of a formal model which Thom introduced before can in the light of a more advanced actor model be interpreted in a way, that it allows all the solutions which Thom claims for his topological minded approach.
Which series of ‘changes’ (maybe ‘catastrophes’) will attract the attention of some researchers, the researcher are every time capable to do the following:
- Write a series of texts representing the observed phenomena at location L and time T in accordance with their learned and agreed meaning functions (a set of propositions).
- This will result in a series of texts (documents) <D1, D2, …, Dn>, whose logical ordering represents the timely order.
- Because every ‘difference’ between two consecutive documents (Di,Di+1) is directly observable in the language expressions one can ‘translate’ these differences directly by a rule following a general format: (i) IF x is a subset of expressions in Di+1, which are not yet members of the set of expressions in Di, THEN ‘add’ these expressions to the set of expressions in Di. (ii) IF y is a subset of expressions in Di, which are no more members of the set of expressions in Di+1, THEN ‘delete’ these expressions from the set of expressions in Di. (iii) Construct a ‘condition-set’ of expressions as subset of Di, which has to be fulfilled to apply (i) and (ii).
- After the translation of all observed differences between consecutive documents one has a set of ‘change rules X’, which together with the ‘Start Document’ D0 define an ‘accumulated rule’ for a series of discontinuous changes: <D0, X>
Probably a first ‘guess’ of an accumulated rules will be not too ‘precise’. Thus by collecting more ‘observations’ one can try to ‘refine’ the rules, even including local probabilities, which during ‘processing’ (inference, simulation) can produce an ‘accumulated and composed’ probability of some ‘weird’ kind.[1]
COMMENTS
[1] This view of composed probabilities is in a good agreement with the ideas of the late Karl Popper discussing ‘propensities’ (see several posts in this uffmm.org blog: https://www.uffmm.org/2021/03/15/philosophy-of-science/)
