eJournal: uffmm.org
ISSN 2567-6458, 19.August 2022 – 19 August 2022
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de
This text is part of the subject COMMON SCIENCE as Sustainable Applied Empirical Theory, besides ENGINEERING, in a SOCIETY. It is a preliminary version, which is intended to become part of a book.
… to be done …
eJournal: uffmm.org
ISSN 2567-6458, 19.August 2022 – 19 August 2022
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de
This text is part of the subject COMMON SCIENCE as Sustainable Applied Empirical Theory, besides ENGINEERING, in a SOCIETY. It is a preliminary version, which is intended to become part of a book.
The words ‘science’, ‘theory’, and ‘scientific theory’ are well known passengers travelling through the times with different meanings, depending from the circumstances, from the minds of different people.[2]-[4] In modern times we have learned a lot about the nature of ‘signs’ and ‘sign-based’ communication as it happens when we are using a ‘language’. And, becoming more sensitive about the dynamics of sign-based communication, we can detect that it is exactly our human use of language which provides the key to a deeper understanding of how our brains are working, located in our bodies, where the brains are playing the roles of ‘spin doctors’ of the pictures in our heads, which are ‘showing’ our mind a ‘virtual world’ of an assumed ‘real world’ somewhere ‘out there’.[14]
Until today we have no final explanation of how exactly this ability of human actors has developed through the times stretching to millions of years ago. And until today there exists no complete description of a living language with the involved structures, meanings, and dynamics. One reason for this ‘fundamental inability’ of describing with a language exactly this language roots is the fact, that language is not a ‘single fixed object’ in front of your eyes, but a dynamic reality happening between many, many different human actors simultaneously; every brain has only some fragments of this assumed ‘whole thing’ called ‘language’, and every communicative act between humans embraces besides ‘rather stable parts’ always a lot of ‘incidental’, ‘casual’ moments of a complex dynamic situation, which constitutes — mostly unconscious — the working of language communication, possible meanings and connotations of meaning. Thus, all the known scientific endeavors until today trying to describe this phenomenon of language communication are more reminding some ‘stuttering’ than a final ‘ordered’ theory.
One lesson we can learn from this tells us, that the so-called ‘everyday language’, the ‘ordinary language’, the ‘natural language’ is the ‘basic’ pattern of language communication. But, as mentioned just before, on account of the fundamental distributed and dynamical character of everyday language, a natural language has no clear cut ‘boundaries’. Never you can tell with certainty where a language ends and where this language just in that moment ‘evolves’, ‘expands’, is ‘changing’.
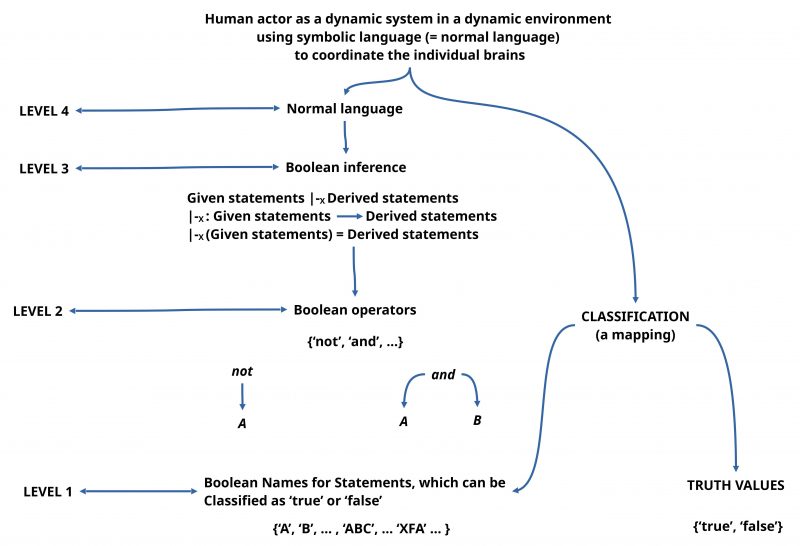
For people which are looking for ‘clear statements’, for ‘finite views’, for a ‘stable truth’ this situation is terrifying. It can cause ‘anxious feelings’. People who like to ‘control’ life don’t like such a ‘living dynamics’ which can not be owned by a single person alone, not even by ‘many’…
One basic property of ordinary language is it’s ‘expandability’: at every time someone can introduce new expressions embedded within new contexts following new patterns of usage. If other human actors start to follow this usage, this ‘new’ behavior is ‘spreading’ through the ‘population of language users’ and by this new growing practice the ordinary language is expanding and thereby changing.
One ‘part’ of ordinary language is called ‘logic’ [6],[7], with various different realizations through history. Another part of ordinary language is ‘mathematics’, especially what is today assumed as being the ‘kernel’ of mathematics, the ‘Theory of Sets’.(cf. [8], [9]) Because ordinary language can always be used to speak ‘about ordinary language’, it is possible to extend an ordinary language with arbitrary many new ‘artificial languages’ like a ‘logic language’ or a ‘mathematical language’.[10] After introducing a special language like a mathematical language’ by using ordinary language one can apply this special language ‘as if it is the only language’, but if you start to ‘look consciously’ to your real practice of speaking, you can easily detect, that this impression ‘it is the only language’ is a fake! Cutting away the ordinary language you will be lost with your special language. The ordinary language is the ‘meta language’ to every special language. This can be used as a ‘hint’ to something really great: the mystery of the ‘self-creating’ power of the ordinary language which for most people is unknown although it happens every moment.
— draft version —
eJournal: uffmm.org
ISSN 2567-6458, 19.August 2022 – 19 August 2022
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de
This text is part of the subject COMMON SCIENCE as Sustainable Applied Empirical Theory, besides ENGINEERING, in a SOCIETY. It is a preliminary version, which is intended to become part of a book.
From the everyday language we know that we can talk ‘about the world’, and even more, we can even ‘act’ with the language. [11] – [13] Saying “Give me the butter, please”, in that case a ‘normal’ [*2] speaker would ‘hear’ the ‘sound of the statement’, he can ‘translate the sound’ into some internal meaning constructs related to the sounds of the language, which in turn will — usually — be ‘matched against’ meaning constructs ‘actually provided’ by the ‘perception’. If there happens to be a ‘sufficiently well match’ then the hearer can identify ‘something concrete’ located on the table which he can associate with the ‘activated language related meaning’ and he then ‘knows’, that this concrete something on the table seems to be an ‘instance’ of those things which are called ‘butter’. But there can exist many different ‘concrete things’ which we agree to accept as ‘instances’ of the meaning construct ‘butter’. Thus, already in very usual everyday situations we encounter the fact, that our perceptions can create signals from ‘something concrete in our perceptions’ and our ‘language-mediated understanding’ can create ‘meaning structures’ which can ‘match’ nearly uncountable different concrete things. [*3] Those meaning constructs — activated by the language, but different from the language — which can match more than one concrete perception, will here be called ‘abstract meaning’ or ‘abstract concept’. And ‘words’ (= expressions) of a language which can activate such abstract meanings are understood as ‘abstract words’, ‘general words’, ‘category words’ or the like. [*4]
Knowing this you will probably detect, that nearly all words of a language are ‘abstract words’ activating ‘abstract meanings’. This is in one sense ‘wonderful’, because the real empirical world consists of uncountable many concrete perceivable properties and to relate every concrete property with an individually matching word would turn the project of language into an infeasible task. Thus with only a few abstract words language users can talk about ‘nearly everything’. This makes language communication possible. The ‘dark side’ of this wonderful ability is the necessity to provide real situations, if you want to demonstrate which of all these concrete properties of a real situation you want to be understood as ‘related’ to the one used word (= language expression) with an abstract meaning. If you cannot provide such ‘concrete situations’ the intended meaning of your abstract words will stay ‘unclear’: they can mean ‘nothing or all’, depending from the decoding of the hearer.
— draft version —
eJournal: uffmm.org
ISSN 2567-6458, 19.August 2022 – 19 August 2022
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de
This text is part of the subject COMMON SCIENCE as Sustainable Applied Empirical Theory, besides ENGINEERING, in a SOCIETY. It is a preliminary version, which is intended to become part of a book.
Talking about ‘butter’ on ‘tables’ during a ‘breakfast’ will usually stimulate lots of ‘imaginations’ in the head of the hearer of such utterances. Because an abstract word can trigger many different ‘concrete things’ these individual imaginations can vary a lot. If different hearers would start to ‘paint’ those imaginations on some paper it could happen, that nearly no two paintings would ‘match’ with all details. The ‘space of possible meanings’ of an abstract word (‘butter’, ‘table’, ‘breakfast’, ‘kitchen’, …) is in principle ‘infinite’. And the manifested ‘diversity’ of the details reveals a kind of ‘fuzziness’ which at a first glance seems to be ‘infeasible’ in the practice of language communication.
This appearing diversity, fuzziness in the examples points to some ‘internal mechanism’ in our brains which works in complete ‘silence’, always ‘automatically’, completely ‘unconscious’, which ‘arranges’ the many different perceptions in a way, which selects some finite set of properties out of the many perceived properties and makes such a ‘selection’ to a kind of ‘signature’, ‘address’, which starts to play the ‘role’ of an individual representation for all those possible sets of perceived properties in the future, which are ‘sufficiently well’ ‘similar’ to those ‘signature properties’. The ‘boundaries’ are not sharp; the boundaries can vary; there can grow large ‘clusters of different property sets’ intersecting with this ‘signature set’ but are different otherwise. Thus, there exists a growing meaning structure in our brains which creates a ‘meaning space’, whose elements can be associated in arbitrary many ways.
If my friend Bill starts talking with me by asking whether there already is some butter on the table, than his utterance — a question — will trigger in me a subset of possible meanings of butter which are in my memory available. Then, when I am looking to the table in the kitchen, I will ‘scan’ the table whether there is something concrete which will ‘match’ these activated internal meanings. Either there happens a direct match or there is something, which looks like something, which feeds back through my perception and urging my memory to ‘look for something alike’. If this happens, then there will be a match too. Thus if such an internal match between ‘perceived properties’ and ‘remembered properties’ will happen then I would shout to Bill “Yes, there is already some butter on the table”. If no such match would happen, then I would shout back “No, there is not yet butter on the table”. In the first case we are used to classify a statement as ‘true’, if the abstract meaning matches a concrete perception sufficiently well; otherwise not. If Mary standing nearby the table would have said before “No, there is no butter on the table” while Jeremy has stated that there is some butter, then these two statements would ‘contradict’ each other. If Jeremy and Mary can come to a common opinion by observable evidence that there is some butter on the table or not, they would be able to ‘agree’ to the positive, affirmative statement that there is some butter on the table, otherwise not. To classify a statement as being ‘false’ would presuppose that the contradicting format of this statement is classified as being ‘true’. If the human actors can not come to a sufficient agreement whether either the statement “Yes, there is already some butter on the table” is true or “No, there is no butter on the table”, then both statements are ‘undecidable’ by the human actors with regard to some observable evidence. In that case these statements are with regard to being ‘true’ or ‘false’ ‘undefined’.[*5]
This everyday situation offers some more variants. If for instance Bill is asking Jeremy whether there is some butter on the table it could happen either that Jeremy says ‘no’ because his ‘understanding’ of the word ‘butter’ consist of kinds of meaning which are not matching that concrete thing on the table, which Bill would understand as ‘butter’. Such a ‘misunderstanding’ can happen easily if people from different cultures are coming together. Thus, having some observable evidence does not guarantee the right classification within a certain language if the language users have learned ‘different meanings in their memory’. In the other case, if Mary has a bad visual perception on account of some ‘visual handicap’ but has in principle the same meaning space like Bill, then it can happen too that she would deny that there is some butter on the table because her visual perceptions are ‘disturbed by their visual handicap’ in a way that the perceptional key to her memory is not in that format which has to match their remembered language induced meaning.
Thus, in this simple example of a ‘true’ statement there are already several ‘factors’ needed to make a ‘true statement’: (i) a perception which works ‘normal’; (ii) a language meaning which is ‘sufficiently common’; (iii) a ‘successful match’ between an actual observation and the triggered memory based meaning. Every factor (i) – (iii) is not simple, can vary a lot. And there exists even more factors which can influence the final classification of being ‘true’ or not; in cases of ‘contradicting statements’ all these different factors can be involved.
In our times of ‘growing fake news’ we can experience, that the agreement between different human persons about the ‘truth’ of a statement can in practice be very difficult or even seems to appear impossible. This points to one more factor which is finally decisive: whatever we perceive and remember, these processes are ’embedded’ in some larger ‘conceptual frameworks‘, which are further ’embedded’ in a system of preferences’ which can be ‘decisive’ for the ‘handling’ of our opinions. Human persons having certain ‘convictions’ related to political or religious or ethical opinions can be ‘driven’ by these convictions in a way, which ‘overrides’ empirical evidences because their ‘conceptual frameworks’ ‘interpret’ these perceptions in a different way. Modern scientific observations are meanwhile often in a format, which only experts can interpret adequately related to a ‘theoretical conceptual framework’. If a non-expert does ‘not trust’ in this scientific interpretation he can ‘switch’ to a different conceptual framework in which he is trusting more, although this other concepOrdinary Language Inference: Preserving and Creating Truthtual framework contradicts the scientific framework, and thus he can assume ‘facts’ which are contradicting those ‘facts’ classified as scientific. Scientists can classify these other facts as ‘fake news’, but this will have no effect on the believer of the fake news. The fake-news believer thinks he is ‘right’ because it matches his individual framework shared by others in social groups.
From this follows that the classification of a statement as being ‘true’ is a complex matter depending from many factors which have to be ‘synchronized’ to come to an agreement. Especially it reveals that ’empirical (observational) evidence’ is not necessarily an automatism: it presupposes appropriate meaning spaces embedded in sets of preferences, which are ‘observation friendly’.
— draft version —
eJournal: uffmm.org
ISSN 2567-6458, 19.August 2022 – 19 August 2022
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de
This text is part of the subject COMMON SCIENCE as Sustainable Applied Empirical Theory, besides ENGINEERING, in a SOCIETY. It is a preliminary version, which is intended to become part of a book.
Every (biological) system which has some sensory input possesses certain states which represent for the system the NOW: that what ‘happens actually’, what is ‘present’ in a mixture of properties and events.
But a NOW provides as such no ‘knowledge’. It is only a NOW.
To ‘overcome’ the NOW a system must be able to map parts of the NOW into other systems states, into such states, which can be ‘recalled’, and which as ‘recalled states’ can be ‘compared’ with the actual NOW. Such a ‘comparison’ can yield ‘similarities’ and ‘differences’. Out of differences distributed over different recalled states ‘sequences of states’ can be constructed’, and sequences of such states can reveal by differences ‘changes’ of properties between consecutive states. With the aid of such sequences revealing possible changes the NOW is turned into a ‘moment’ embedded in a ‘process’, which is becoming the more important reality. The NOW is something, but the PROCESS is more.
— draft version —
eJournal: uffmm.org
ISSN 2567-6458, 19.August 2022 – 19 August 2022
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de
This text is part of the subject COMMON SCIENCE as Sustainable Applied Empirical Theory, besides ENGINEERING, in a SOCIETY. It is a preliminary version, which is intended to become part of a book.
In this enlarged reality of a process the ability to generate ‘signatures’ representing ‘some properties’ out of a set of properties, is the other ‘magic’ tool to compose ‘abstract structures’ which can be expanded if necessary, which can be related to nearly everything; an abstract structure can become associated with other structures, can be embedded in ‘hierarchic’ structures, and even more. Abstract structures are the other ‘tools’ to overcome the NOW: ‘reality’ is not only ‘what is now’, but in the same time also that what can be added, extended, combined to the given structure. Abstract structures are as part of an embracing process ‘potentials’, ‘possible alternatives’, something which can become ‘true’ in some following state, that means in some ‘possible future.’
If someone has introduced the word ‘cup’ for something concrete which allows to hold some fluid, which can be used to ‘drink’ out of this concrete something, the word ‘cup’ — an expression of some language — is not a fixed, static object but — as part of a possible process — can be used to ‘touch’ more and more different concrete objects allowing them to become ‘part of the internal meaning structure’ of a speaker-hearer. Thus while the ‘word’ as language expression stays ‘the same’ the associated meaning space can change, can grow, can shrink, can be associated with other meaning spaces.
In this sense seems ‘language’ to be the master tool for every brain to mediate its dynamic meaning structures with symbolic fix points (= words, expressions) which as such do not change, but the meaning is ‘free to change’ in any direction. And this ‘built in ‘dynamics’ represents an ‘internal potential’ for uncountable many possible states, which could perhaps become ‘true’ in some ‘future state’. Thus ‘future’ can begin in these potentials, and thinking is the ‘playground’ for possible futures.(but see [18])
— draft version —
eJournal: uffmm.org
ISSN 2567-6458, 19.August 2022 – 20 August 2022
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de
This text is part of the subject COMMON SCIENCE as Sustainable Applied Empirical Theory, besides ENGINEERING, in a SOCIETY. It is a preliminary version, which is intended to become part of a book.
(Has to be re-written)
We know from everyday life and partially from science that this ability of abstract potentials as part of possible processes can under certain conditions be used for ‘forecasts’ with important practical consequences: for the Egyptian people it was of high importance to know in advance when the floods of the Nil river would arise again. Generally it was important to understand the different periods of the year, the process of time, or the connections between food and effects on our bodies, or the ‘art of agriculture’ to prepare for enough food for all people, and much more.
With the reality of being part of a process with a NOW, with the ability to overcome the NOW by generating abstractions, sequences of states, and recognizing changes, with the ability to derive ‘possible follow-up states’ out of the known sequences of states, it is generally possible to produce forecasts.
But not any forecast is ‘helpful’.
If the experts say that in two weeks the floods of the river will come, but this would not happen, it would not be appreciated; if people recommend certain food for your health and you will become ill, it would not be appreciated either. Thus forecasts should possess the property, that the state, which is ‘announced to become true’, indeed would become ‘true’. ‘True’ means here that the ‘announced state’ will at some ‘point in the future’ be ‘instantiated by some real facts which can be observed.
This leads to the interesting question, how it is possible to ‘derive’ from some ‘given states’ in the memory ‘possible states’ in the memory, which have the potential to become in some time ‘instantiated’ in a way, which makes them ‘real’ and thereby ‘observable’.
In modern formal logic language expressions are well defined expressions of some language but ‘without any concrete meaning’. The only assumed property of logical statements is the property to be called ‘true’ or ‘false’ without relating these abstract properties to some real meaning. Thus you can play with these ‘logical expressions’ in a purely formal way by defining some rules, how one can change an expression and under which conditions the transformation of a set of given expressions into another set of expressions is called a ‘logical derivation’ which preserves the ‘abstract trues’ of the assumed primary set of expressions. These are nice games allowing numerous different kinds of definitions of ‘logical derivation’ without any real relation to everyday language and meaning. All the known examples how to use formal logic applied to everyday meaning until today are not really convincing. The numerous articles and even books dealing with such examples can only work, if we forget nearly everything which we know about our everyday world. This seems to be a strange deal.
If one instead looks to the way human actors are making forecasts in the everyday world without using formal logic one can detect, that this is not only possible, it seems to be the only powerful way to do it.
— draft version —
eJournal: uffmm.org
ISSN 2567-6458, 19.August 2022 – 19 August 2022
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de
This text is part of the subject COMMON SCIENCE as Sustainable Applied Empirical Theory, besides ENGINEERING, in a SOCIETY. It is a preliminary version, which is intended to become part of a book.
In the following examples four languages are used simultaneously: (i) Boolean logic, (ii) German language, (iii) English language, (iv) Predicate logic. The idea is to make ‘visible’ that formal logic provides not only a very limited profit, but that the normal language can offer all what formal logic can offer, but even much more. If one keeps in mind that the ‘normal’ language is principally the meta-language for every kind of ‘special’ language then this should be no surprise.
— draft version —
eJournal: uffmm.org
ISSN 2567-6458, 19.August 2022 – 19 August 2022
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de
This text is part of the subject COMMON SCIENCE as Sustainable Applied Empirical Theory, besides ENGINEERING, in a SOCIETY. It is a preliminary version, which is intended to become part of a book.
In the language of boolean logic — also called ‘propositional logic’ (but see [17]) — we have only expressions for ‘names’ of statements — like ‘A’, ‘B’, ‘CD’, … — , which can be classified (on a meta-level!) as being ‘true‘ or ‘false‘.
Whether one of the used names for statements is ‘true’ or ‘false’ has to be explained ‘separately’ — on a meta-level! — often written in a list or table called ‘truth table’ like:
Further we have some expressions naming ‘logical operators’ which we write here as ‘not‘ and ‘and‘. Strictly speaking these are on a ‘meta-level’ compared to the expressions representing statements which can be true or false.
Thus we could write the compound statement ‘A and B and C’
claiming that the whole expression has the meta-property of being true independent which truth values the individual statement expressions B’ and ‘C’ are assumed to have.
This simultaneous occurrence of two different meta-levels in the description of boolean logic expressions raises the question, how these metal-levels are ‘interacting’? The discussion of this question will be postponed here until we have discussed what is called a ‘logical derivation’.
A ‘logical derivation rule’ tells us that if we have an expression like ‘A and B’ ‘assumed’ to be ‘true’ than we can ‘derive’ from this expression that the expression ‘A’ or ‘B’ alone is also ‘true’. Thus with our introductory example, that the expression A and B and C is assumed to be true, we could ‘logically derive’ that the expressions A, or B, or C taken ‘alone’ are true either. In the logical meta-language we could describe this derivation relation as
A and B and C ⊢X A
or
A and B and C ⊢X B
or
A and B and C ⊢X C
where the sign ⊢X denotes the logical derivation operator (meta-level !) with the arguments (left side) A and B and C and (right side) A or B or C. The index sign ‘X’ represents the set of derivation rules. In this case we have only one rule, therefore X = {if we have an expression like ‘A and B’ ‘assumed’ to be ‘true’, than we can ‘derive’ from this expression that the expression ‘A’ or ‘B’ alone is also ‘true’}
Coming back to the question of the interplay between the meta-level assumption that the expression C is assumed to be false but can be derived from the compound statement A and B and C as being ‘true’ reveals that the property of being ‘false’ of an individual statement and the property of an individual statement ‘C’ to be in a logical derivation ‘true’ describes apparently two different properties.
A possible solution of this meta-problem can be to introduce the convention, that the ‘individual true-false qualification’ can be expressed by ‘C’ as encoding ‘C is true individually’ and ‘not C’ as encoding ‘C is false individually’. But this ‘convention’ will only work if it would be ‘done’ before’ a logical derivation (again a meta-level matter). Thus, if one assumes the individual true-false qualifications of the before mentioned truth-table as ‘given’, than we had to write the compound statement as
A and not B and not C
which could yield the following derivations
A and not B and not C ⊢X A
or
A and not B and not C ⊢X not B
or
A and not B and not C ⊢X not C
Thus we have presupposed ‘individual truth values’ and then one can logically derive either ‘B’ or ‘not B’ as ‘logically true’.
This discussion of ‘individual truth values’ compared to ‘logically derived truth values’ raises confusion. Indeed, boolean logic as such takes only names for expressions like ‘A’ or ‘B’ as arguments for their logical operators — ‘not’, ‘and’, … — being fed into a logical derivation relation — ⊢X — without taking into account individual truth values. This part is ‘delegated’ to the user of boolean logic; the possible ‘interpretation’ of boolean logic expressions’ with ‘real truth’ is ‘outside of boolean logic’!
The leading idea is therefore that the usage of a symbolic language has to be understood as an interaction of several ‘levels of meaning’ simultaneously. One single language expression can be seen from the perspective of ‘meaning’ (the adaptive built function in every human actor) as having several ‘levels of meaning’. In the case of boolean logic this are at least four levels.
More aspects of the case of boolean logic will be discussed in the following sections.
— draft version —
eJournal: uffmm.org
ISSN 2567-6458, 19.August 2022 – 19 August 2022
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de
This text is part of the subject COMMON SCIENCE as Sustainable Applied Empirical Theory, besides ENGINEERING, in a SOCIETY. It is a preliminary version, which is intended to become part of a book
In the following example we have a human actor being part of a traffic situation, who gives some fragments of a language description of what he is experiencing (in the next section this example will be given with the English language).
In a first situation the human actor would say:
“Die Ampel zeigt rot.”
Some seconds (or minutes) later he would state:
“Die Ampel zeigt orange.”
Again, after some seconds (or minutes) he would utter:
“Die Ampel zeigt grün.”
Then he would start to move away.
We could ‘name’ these expressions by abbreviation in the following way:
A := “Die Ampel zeigt rot.”
B := “Die Ampel zeigt orange.”
C := “Die Ampel zeigt grün.”
In the everyday situation where these statements will be uttered by a human actor this human actor would classify each statement as ‘being true’, because the ‘known meaning’ associated with these expressions is in that moment of being uttered in a ‘sufficient accordance’ with the perceived situation. Thus, one could classify the individual statements as ‘true’ while being ‘uttered’.
Using the abbreviations ‘A’, ‘B’, and ‘C’ we could apply the inference machinery of the boolean logic with
(1) A and B and C ⊢X A or … B … or C
In the everyday situation where these statements have been uttered this logical inference would be wrong. If we would do it like in (1).
The reason for this insufficiency is grounded in the fact, that each statement from ‘A’, ‘B’, and ‘C’ is describing the property of a traffic light (being red, orange or green), and only one of these statements can be true at a certain point of time. Thus the ‘truth’ of these statements is ‘time dependent’! Furthermore works the traffic sign in an ‘action pattern’ which makes one ‘color’ ‘true’ and at the same time all other colors ‘false’. Thus a traffic light is a collection of statements like this:
(2) traffic light := {‘A and non B and non C’ or ‘non A and B and non C’ or ‘non A and non B and C’} (with ‘or’ as another boolean operator).
From this the following boolean derivations would be possible:
From the boolean derivation as such it would not be possible to decide, which of the possible variants would be the case in a certain moment. Because boolean logic in general has to assume a human actor (or any kind of actor with sufficient properties), who is able to associate the expressions with his internal meaning space, combined with the intention to classify which of the ‘logically possible variants’ is matching an ‘actual situation’, which offers those ‘meaning properties’, which are needed, to ‘make the expression an instance’ of this meaning case.
Naturally, it is a human actor who has to ‘invent’ the definition of a ‘traffic light’ in the format of (2), if he knows concrete examples of traffic lights in everyday situations. Because of this, because a human actor has an internal knowledge space with an internal meaning function μ, he ‘knows’ which kinds of properties are ‘related’ to that what is called a ‘traffic light’. And from this follows with ‘normal logic’ that
— draft version —
eJournal: uffmm.org
ISSN 2567-6458, 19.August 2022 – 19 August 2022
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de
This text is part of the subject COMMON SCIENCE as Sustainable Applied Empirical Theory, besides ENGINEERING, in a SOCIETY. It is a preliminary version, which is intended to become part of a book.
The foregoing comparison of derivations in a ‘boolean logic setting’ and in an ‘everyday language setting’ shows a remarkable difference: while the inventors of boolean logic focused on formal expressions only by cutting of all ‘natural meaning’, the ‘inventor’ of natural language — the whole biosphere! — created ‘normal language’ to be a ‘medium’ to encode the ‘internal states’of the sending brain into expressions which can be transmitted to other brains which as ‘receivers’ should be able to ‘decode’ these expressions into the internal states of the receiving brains. Thus ‘expressions as such’ are of nearly no help for the survival of brains. Survival needs cooperation between different brains and the only chance to enable such cooperation is communication of internal states by ‘encoded expressions’.
From this follows that ‘natural logic’ has to follow completely different patterns than ‘boolean logic’. Let us look to the example again.
We continue using the before introduced abbreviations A := ‘Die Ampel zeigt rot’ etc.
In figure 3 a simple ‘sequence of states’ has been outlined where the usual sequence of showing ‘red’, ‘orange’, and green is assumed. In certain types of cultures this is a typical everyday situation.
Thus we can assume a ‘state S1’ where the traffic light is showing ‘red’. This can be represented by the expression:
A
All participants know, that this expressions describes a real situation where the ‘learned meaning of this expression’ is in accordance with the actual ‘perceptions’ which are assumed to be in ‘accordance’ with some ‘real situation outside the brain and outside the body’. In that case the ‘speaker’ and ‘hearer’ of expression ‘A’ agree – under normal circumstances — that the ‘meaning’ associated with the expression ‘A’ is ‘true’. If the perception would provide ‘another concrete construct’ triggered by a traffic light showing ‘orange’ instead of ‘red’ then the learned meaning of expression ‘A’ would not match. In that mismatch situation speaker and hearer would agree – under normal circumstances — that the ‘meaning’ associated with the expression ‘A’ is ‘not true’, and this is a case of being classified as ‘false’.
Now, what could in such a situation be a ‘derivation’ in the context of a ‘natural logic’?
As has been mentioned before the ‘abstract structures’ of the meaning space are ‘dynamic constructions’ allocating many different properties of the perceived real world into ‘internal (neural = cognitive) clusters’ representing these properties within these structures. Thus, the abstract structure ‘traffic light’ is a structure possessing the typical collection of three different lights with their typical pattern of sequential activations.[19] A brain which has built up such abstract structures can use these to produce ‘forecasts’ by ‘reading its learned structures’!
Assume that the perceived situation is that state called S1 which can be described with the expression ‘A’:
S1 = {A}
From the learned abstract structure ‘traffic light’ the brain could ‘derive the rule’
R1:
IF there is a situation S which has a property described by an expressions ‘A’, THEN it can happen in a follow up state S’, that the expression ‘A’ does not any more match’, but expression ‘B’.
If we make the set of derivation rules X equal to the set comprising rule R1 with X = {R1} then we can built the following natural logic derivation:
S ⊢X S’
with S ={A} and S’={B}.
This kind of derivation is radically different to a boolean logic derivation:
(i) While boolean logic can only derive something which is ‘already true’, natural logic can derive something which ‘could become true in the future’ by assuming, that the ‘learned meaning’ is ‘true’.
(ii) While boolean logic can only use derivation rules based on operations with expressions only, natural logic can exploit the vast amount of ‘learned meaning structures’ owned by an individual brain and which is partially ‘shared’ with other brains.
Based on (ii) a brain is always capable to ‘construct its own derivation rules’ simply by ‘exploiting’ its learned abstract (dynamical) structures. Thus every brain can ‘invent’ new types of logic only by using its ‘learned experience’.
From this follows directly that human actors which want to ‘think explicitly about some possible future’ should abandon boolean logic and instead should exercise to exploit their learned knowledge.
In a historical perspective it is very strange that the most advanced complex system of the whole known universe — the biosphere, and as part of it the homo sapiens population — decided to use as logic a system, which abandons all this fantastic inventions of more than 3.5 billion (10^9) years to select a system of sign operations, which is more than pure and of not too much help for survival. The construction of programmable machines (usually called computers) by using boolean logic has enabled an interesting tool, but only if we use this as ‘part of biological intelligence’.
— draft version —
eJournal: uffmm.org
ISSN 2567-6458, 19.August 2022 – 19 August 2022
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de
This text is part of the subject COMMON SCIENCE as Sustainable Applied Empirical Theory, besides ENGINEERING, in a SOCIETY. It is a preliminary version, which is intended to become part of a book.
In this section we repeat the everyday example from before, now with expressions from the English language. The situation is a human actor in front of a traffic light showing a ‘red’ light.
In this situation the human actor could say:
“The traffic light shows red.”
Some seconds (or minutes) later he would state:
“The traffic light shows orange.”
Again, after some seconds (or minutes) he would utter:
“The traffic light shows green.”
Then he would start to move away from the traffic light.
We could ‘name’ these expressions by abbreviation in the following way:
A := “The traffic light shows red.”
B := “The traffic light shows orange.”
C := “The traffic light shows green.”
After the introduction of these abbreviations this example looks completely as the example with the German expressions. And, indeed, it works completely similar. The reason for this is located in the ‘body system’ of a human actor with its special ‘brain’.
n the following example we have a human actor being part of a traffic situation, who gives some fragments of a language description of what he is experiencing (in the next section this example will be given with the English language).
In a first situation the human actor would say:
“Die Ampel zeigt rot.”
Some seconds (or minutes) later he would state:
“Die Ampel zeigt orange.”
Again, after some seconds (or minutes) he would utter:
“Die Ampel zeigt grün.”
Then he would start to move away.
We could ‘name’ these expressions by abbreviation in the following way:
A := “Die Ampel zeigt rot.”
B := “Die Ampel zeigt orange.”
C := “Die Ampel zeigt grün.”
In the everyday situation where these statements will be uttered by a human actor this human actor would classify each statement as ‘being true’, because the ‘known meaning’ associated with these expressions is in that moment of being uttered in a ‘sufficient accordance’ with the perceived situation. Thus, one could classify the individual statements as ‘true’ while being ‘uttered’.
Using the abbreviations ‘A’, ‘B’, and ‘C’ we could apply the inference machinery of the boolean logic with
(1) A and B and C ⊢X A or … B … or C
In the everyday situation where these statements have been uttered this logical inference would be wrong. If we would do it like in (1).
The reason for this insufficiency is grounded in the fact, that each statement from ‘A’, ‘B’, and ‘C’ is describing the property of a traffic light (being red, orange or green), and only one of these statements can be true at a certain point of time. Thus the ‘truth’ of these statements is ‘time dependent’! Furthermore works the traffic sign in an ‘action pattern’ which makes one ‘color’ ‘true’ and at the same time all other colors ‘false’. Thus a traffic light is a collection of statements like this:
(2) traffic light := {‘A and non B and non C’ or ‘non A and B and non C’ or ‘non A and non B and C’} (with ‘or’ as another boolean operator).
From this the following boolean derivations would be possible:
From the boolean derivation as such it would not be possible to decide, which of the possible variants would be the case in a certain moment. Because boolean logic in general has to assume a human actor (or any kind of actor with sufficient properties), who is able to associate the expressions with his internal meaning space, combined with the intention to classify which of the ‘logically possible variants’ is matching an ‘actual situation’, which offers those ‘meaning properties’, which are needed, to ‘make the expression an instance’ of this meaning case.
Naturally, it is a human actor who has to ‘invent’ the definition of a ‘traffic light’ in the format of (2), if he knows concrete examples of traffic lights in everyday situations. Because of this, because a human actor has an internal knowledge space with an internal meaning function μ, he ‘knows’ which kinds of properties are ‘related’ to that what is called a ‘traffic light’. And from this follows with ‘normal logic’ that
— draft version —
eJournal: uffmm.org
ISSN 2567-6458, 19.August 2022 – 19 August 2022
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de
This text is part of the subject COMMON SCIENCE as Sustainable Applied Empirical Theory, besides ENGINEERING, in a SOCIETY. It is a preliminary version, which is intended to become part of a book.
So-called ‘predicate logic’ can be found since the classical Greek philosophy (cf. [7], chapter 2), but in the ‘old times’ not in the format which we know and are using since Frege, Russel & Whitehead and others since the 20th century.
What one can observe in the talking about predicate logic is a constant reduction of the properties of predicate logic as well as the circumstances of usage. While we can find in the collection of texts associated with Aristotle called ‘Organon’ different dimensions beyond the pure expressions — in a not complete systematic way — do modern texts restrict themselves more or less to expressions only …. in theory, not in practice.
To discuss the topic of predicate logic in an everyday setting we will start with predicate logic from the point of view of expressions only and then we will try a look to the ‘conditions of usage’.
In the outline presented in figure 4 we take as a common assumption that human actors are the main actors producing and using predicate logic. From these human actors we know that they are ‘complex dynamic systems’ living in a complex dynamic environment (with the human actors as part of this environment making it even more complex than without human actors). Furthermore it is a historical fact that the homo sapiens population demonstrates since its beginning (before about 300.000 years somewhere in Africa) the special ability that their brains — embedded in their bodies — can organize a ‘communication by symbolic means’ in a way which enables these individual distributed brains to ‘coordinate’ the ‘behavior’ of their bodies in a growing complex manner. History shows how the ‘technology of communication’ has changed constantly beginning with written symbols, texts, libraries, data bases, connected data bases within computer networks called ‘cyberspace’.
Besides many thousands of ‘ordinary (= normal) languages’ the brains of the homo sapiens population have invented many ‘specialized languages’ extending the normal languages in many directions. Such a specialized language’ is completely depending from the given normal language. Without the used natural language a specialized language cannot exist; a specialized language as such is ‘nothing’; with a normal language as starting point a specialized language can allow quite complex ‘artificial symbolic structures’ which — used in an ‘adequate manner’ — can help the acting brains to ‘describe possible meanings’ which can eventually help to understand some parts of the ‘perceivable world outside the brain’ (and thereby some behavior of the brain itself!)
— draft version —
eJournal: uffmm.org
ISSN 2567-6458, 19.August 2022 – 19 August 2022
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de
This text is part of the subject COMMON SCIENCE as Sustainable Applied Empirical Theory, besides ENGINEERING, in a SOCIETY. It is a preliminary version, which is intended to become part of a book.
From the section about Boolean Logic we know, that there can be expressions called ‘statements’ which can be classified as being ‘true’ or ‘false’ without describing what ‘true’ or ‘false’ means. An ‘interpretation’ of a ‘possible meaning’ of the expressions ‘true’/’false’ is a property of the human actor dealing with these statements. We as human speakers ‘know’ by ‘experience’, that the classification of an expression as being ‘true’ or not depends from our ‘interpretation’ of the expression ‘A’ whereby the interpretation activates a ‘known meaning’ which can be related so some ‘assumed world of references’. Thus the usage of Boolean logic is a way of ‘short, condensed notation’ of a possible high complex ‘knowledge’ of the human actor using this notation. Without this assumed knowledge of the human user the notation makes no sense.
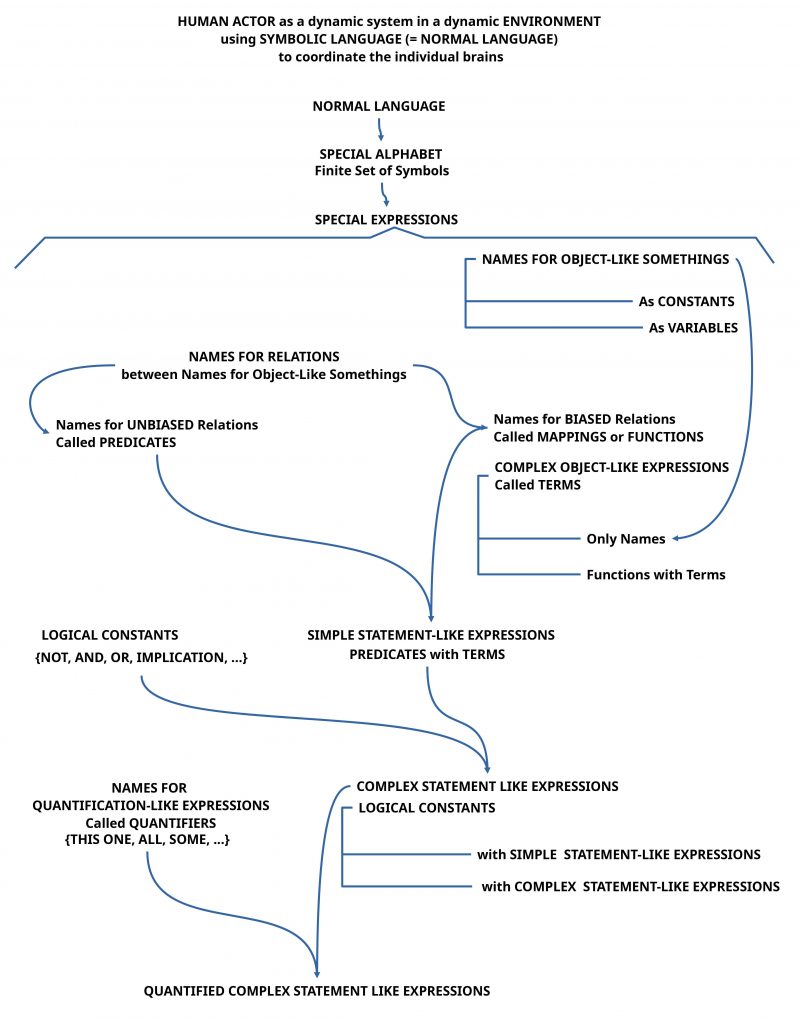
In the case of predicate logic the situation is similar, but also different. Predicate logic offers also a notation for expressions called statements which possibly can be classified as being ‘true’ or ‘false’, but in the case of predicate logic these notations are not only ‘names’ of some expressions but they show a minimal ‘expression-inherent structure’.
Figure 4 shows that the ‘minimal format’ of a predicate logic expression called statement includes at least one ‘predicate’ and at least one ‘term’, where the term is minimally represented by a ‘name’ of an ‘object-like something’, and this name is a ‘constant’. An expression is called a ‘constant’ when it is related to a ‘known reference’, which can be related to something concrete, which gives a human actor the possibility to ‘decide’ that there ‘exists’ an ‘observable something’ which can be understood as an ‘instance’ of the ‘known reference’. Thus one can see that in the case of predicate logic too one has to assume a sufficient ‘knowledge’ inside the human actor which enables a sufficient ‘interpretation’ along with the possibility to ‘decide’ whether this ‘name’ is a constant or not.
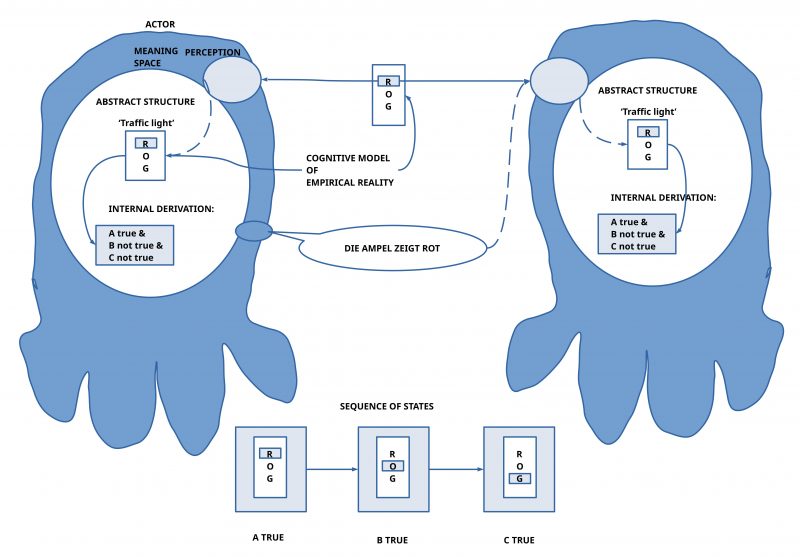
(Example 1) IS-RED(traffic-light-number-111)
Example 1 shows an example of a simple statement in a predicate logic format with the term ‘traffic-light-number-111’ as a name used as a constant pointing to some assumed decidable object-like something located somewhere in the city related to the predicate expression ‘IS-RED’ with the possible meaning of ‘showing the color red’.
Such an expression with an interpretable predicate expression as well an interpretable name as term can be classified as being ‘true’ if the ‘known meaning’ of this expression, which is assumed within an interpretation, can be related to some ‘observable object-like something’ which ‘matches’ the properties of the known meaning. In this sense the expression of Example 1 can be understood as a ‘notation’ which can be associated with a known meaning by interpretation, which in turn can be ‘verified’ or ‘falsified’, or not. In the last ‘undecidable case’ either there is no ‘observable instance’ available or there is no ‘clear knowledge’ available.
The expressions used here like ‘known meaning’ or ‘object-like something’ or ‘interpretation’ (and others) are not part of predicate logic itself but belong to the ‘meta theory of logic’ — short: meta-logic — which is rooted in the ‘general everyday knowledge’, which has to be assumed as ‘general condition’ for any special thinking. Either it is there and ‘works’ or not. If not, the human actors have no chance to discuss these topics in some way. This kind of ‘primary knowledge’ can be compared to the case of the ‘body’ and therein the ‘brain’ as a ‘something given’, which enables certain real processes which you can ‘use’ by ‘living these’, but without brain or body you are simply ‘not there’. Take it or leave it. If you ‘take it’ then you can do something, e.g. you can use a language associated with some ‘known meaning’ which enables you to ‘relate’ language expressions to ‘something else’ functioning as ‘reference’.
Another more complex format of a predicate logic statement is one where more than one simple predicate occurs:
(Example 2) IS-RED(traffic-light-number-111) AND NOT(IS-ORANGE(traffic-light-number-111)) AND NOT(IS-GREEN(traffic-light-number-111))
In this simple example do occur three simple predicates ‘IS-RED’, ‘IS-ORANGE’, and ‘IS-GREEN’, all related to the object name ‘traffic-light-number-111’, and logical expressions like ‘NOT’ and ‘AND’. The logical expression ‘NOT’ turns the meaning of an expression to the opposite: thus the expression ‘NOT(IS-ORANGE(traffic-light-number-111))’ generates the meaning that the object ‘traffic-light-number-111’ does not show the color ‘orange’ (leaving it undefined, what it could mean not to be ‘orange’! The space of possible other meanings is inherently ‘fuzzy’ and can be ‘large’) . The logic expression ‘AND’ generates a ‘compound meaning’ like ‘IS-RED(traffic-light-number-111) AND NOT(IS-ORANGE(traffic-light-number-111))’. This compound statement generates the known meaning, that the object ‘traffic-light-number-111’ shows the read light and at the same time ‘not’ the orange light. If this is the observable case, then this compound statement would be classified as ‘decidable true’, otherwise not.
If one would use within predicate logic expressions not ‘constants’ like ‘names’ but ‘variables’, then the situation changes.
(Example 3) IS-RED(x) AND NOT(IS-ORANGE(y)) AND NOT(IS-GREEN(z))
A ‘variable’ as such has no known ‘meaning’ and therefore will never be able to be associated with a decidable observable something. Thus to turn a predicate logic expression with variables into a real candidate for being classified as ‘true’ or ‘false’ (or undefined), one has to offer a procedure how to replace the variables by expressions, which can become ‘truth candidates’. A common format for such a procedure is the ‘replacement’ (often called ‘substitution’) of the expression called ‘variable’ by an expression called ‘constant’ like ‘x’ will be replaced by ‘traffic-light-number-111’, written: (x/traffic-light-number-111).
In case of predicate logic there exists one more ‘formal element’ to modify the possible meaning: Quantifiers! To say ‘ALL (x)’ or ‘ONE (x)’ or ‘SOME (x)’ or ‘EXACT n (X)’ and the like gives some ‘clue’, to the assumed ‘number’ of object-like somethings which have to be shown to ‘be there’ in a ‘decidable manner’.
Thus it makes a difference whether one writes ‘ALL(x)’ in the case of ‘IS-RED(x) AND NOT(IS-ORANGE(y))’ or ‘ALL(x,y)’. If one in the first case ‘ALL(x)’ replaces (x/traffic-light-number-112) then one derives the expression ‘IS-RED(traffic-light-number-111) AND NOT(IS-ORANGE(y))’, where the variable ‘y’ is still undefined. In the second case with ‘ALL(x,y)’ one will derive by (x/traffic-light-number-112) and (y/traffic-light-number-113) the expression ‘IS-RED(traffic-light-number-111) AND NOT(IS-ORANGE(traffic-light-number-113))’; all variables have been replaced.
In case of Example 3, where the used variable {x,y,z} are as expressions ‘different’, one can speak potentially about three different traffic lights using the replacements (x/traffic-light-number-111), (y/traffic-light-number-112), (z/traffic-light-number-113):
(Example 3.1) IS-RED(traffic-light-number-111) AND NOT(IS-ORANGE(traffic-light-number-112)) AND NOT(IS-GREEN(traffic-light-number-113)
If these different traffic lights would be distributed at different places in the city then it could become more and more difficult if not even infeasable, to observe these objects in a decidable way simultaneously. To use technological means to solve the problem can work ‘in principle’ by using such ‘technological means’, but then the technological means have to be ‘proven’ to work ‘correctly’ (they have to be ‘certified’). Who can and will do this?
This example demonstrates that the formal status of an expression — having constants instead of variables — enables ‘principally’ a decision procedure between the actors, but by ‘practical conditions’ this ‘formal possibility’ can often not be resolved in the domain of ‘real usage’.
Such a case of ‘theoretical decidable’ but ‘practical undecidable’ is also given if one uses the quantifier ‘ALL (x, …)’ where the number of ‘possible real candidates’ is by practical reasons not really decidable, e.g. ‘All human persons are at 10:00 a.m. the upcoming Monday not hungry’, written as ‘ALL (x) HUMAN-PERSON(x) AND (NOT(IS-HUNGRY(x)) AND DATE(next(Monday)) AND CLOCK(10, a.m.)’. In this example ‘Monday’ is related to a ‘calendar’ and ‘next()’ is a function mapping the actual day in the calendar to the next available Monday. The possible real instances of the variable ‘x’ are assumed as ‘all living human persons on the planet earth 17.July 2022’. Actually we have no measurement procedure to decide all these statements.
If one uses the quantifier ‘ONE()’, then one introduces a ‘restriction’ to the umber of possible instances where the whole number of possible real candidates shall be ‘one’:
(Example 3.2) ONE(x) IS-RED(x) AND NOT(IS-ORANGE(x)) AND NOT(IS-GREEN(x))
The ‘meaning of the quantifier ‘ONE()’ is assumed here as ‘There must exist one object-like something, which is a candidate for the known meaning’.
If we assume the replacement (x/traffic-light-number-111) then we get the expression
(Example 3.2.1) ONE(x/traffic-light-number-111)(IS-READ(traffic-light-number-111) AND NOT(IS-ORANGE(traffic-light-number-111)) AND NOT(IS-GREEN(traffic-light-number-111))
This expression can become classified as ‘true’ observing the traffic light in place.
The final aspect of predicate logic expressions — which we already have used in the ‘next Monday’ example — are the ‘terms’ in predicate logic. A term is in the simple case (i) only one variable or a constant replacing the variable, or (ii) a ‘function’ — often called ‘operator’ — with some ‘arguments’ like ‘add(1,3)’ or ‘multiply(4,7)’ or ‘father-of(John)’ or ‘phone-number-of(Bill)’ or the like. A function is a ‘biased relation’ mapping some object-like things to other object-like things. Because a certain customer of a phone-company has usually exactly one phone-number one can resolve ‘phone-number-of(Bill)’ by looking to the list of phone-numbers of this company (or you know the number already). The expression ‘father-of()’ works similarly. ‘Multiplying’ two numbers is described in a part of mathematics giving strict rules how to multiply two numbers, thus following these rules you will get ‘one number’ as the ‘result’ of this operation like ‘multiply(4,7)=28’. Because a function applied to object-like somethings produces again an object-like something the function stays as a term in the realm of object-like somethings. Thus in an expression like ‘ONE(x) FATHER(father-of(x))’ one uses the function ‘father-of()’ to denote that one object-like something which is the father of x to make the statement, that this ‘father-of(x)’ has the property of being a ‘father’ written as ‘FATHER()’. While the function ‘father-of()’ determines exactly one biological object-like something the predicate ‘FATHER()’ can be applied to many different object-like somethings, e.g. ‘ONE(x) ONE(y) FATHER(father-of(x)) AND FATHER(father-of(y))’ , replacing (x/Bill), (y/Susan) then ‘FATHER(father-of(Bill)) AND FATHER(father-of(Susan))’ the function father-of() generates two different object-like somethings but the predicate FATHER() can be applied to both of them.
— draft version —
eJournal: uffmm.org
ISSN 2567-6458, 19.August 2022 – 19 August 2022
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de
This text is part of the subject COMMON SCIENCE as Sustainable Applied Empirical Theory, besides ENGINEERING, in a SOCIETY. It is a preliminary version, which is intended to become part of a book.
From the examples of boolean logic and predicate logic we can see that formal logic is operating with a set of expressions assumed to be true and then offers some rules how one can derive from this set of assumed true expressions some concrete expressions. The whole inference mechanism works strictly ‘conservative’ in the sense that it is not possible to ‘create’ by logical inference ‘something new’. Formal logical inference is preserving the truth.
— draft version —