eJournal: uffmm.org
ISSN 2567-6458, 2.April – 2.April 2021
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de
CONTEXT
This text is part of a philosophy of science analysis of the case of the oksimo software (oksimo.com). A specification of the oksimo software from an engineering point of view can be found in four consecutive posts dedicated to the HMI-Analysis for this software.
THE OKSIMO THORY PARADIGM
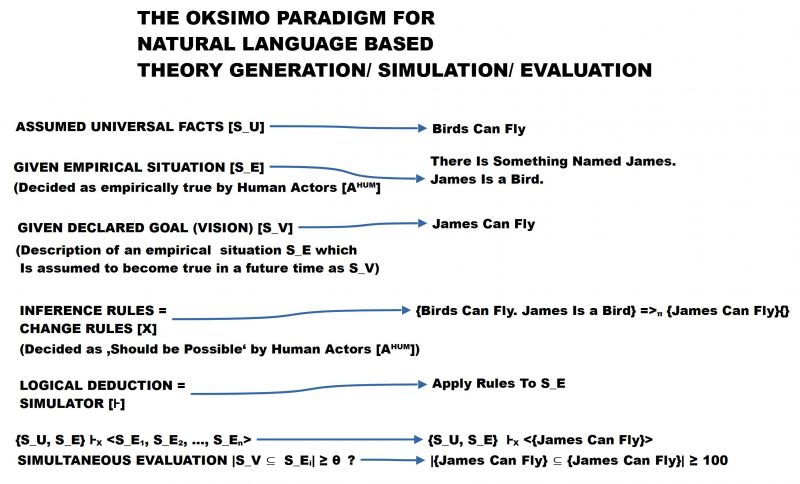
The following text is a short illustration how the general theory concept as extracted from the text of Popper can be applied to the oksimo simulation software concept.
The starting point is the meta-theoetical schema as follows:
MT=<S, A[μ], E, L, AX, ⊢, ET, E+, E-, true, false, contradiction, inconsistent>
In the oksimo case we have also a given empirical context S, a non-epty set of human actors A[μ] whith a built-in meaning function for the expressions E of some language L, some axioms AX as a subset of the expressions E, an inference concept ⊢, and all the other concepts.
The human actors A[μ] can write some documents with the expressions E of language L. In one document S_U they can write down some universal facts they belief that these are true (e.g. ‘Birds can fly’). In another document S_E they can write down some empirical facts from the given situation S like ‘There is something named James. James is a bird’. And somehow they wish that James should be able to fly, thus they write down a vision text S_V with ‘James can fly’.
The interesting question is whether it is possible to generate a situation S_E.i in the future, which includes the fact ‘James can fly’.
With the knowledge already given they can built the change rule: IF it is valid, that {Birds can fly. James is a bird} THEN with probability π = 1 add the expression Eplus = {‘James can fly’} to the actual situation S_E.i. EMinus = {}. This rule is then an element of the set of change rules X.
The simulator ⊢X works according to the schema S’ = S – Eminus + Eplus.
Because we have S=S_U + S_E we are getting
S’ = {Birds can fly. Something is named James. James is a bird.} – Eminus + Eplus
S’ = {Birds can fly. Something is named James. James is a bird.} – {}+ {James can fly}
S’ = {Birds can fly. Something is named James. James is a bird. James can fly}
With regard to the vision which is used for evaluation one can state additionally:
|{James can fly} ⊆ {Birds can fly. Something is named James. James is a bird. James can fly}|= 1 ≥ 1
Thus the goal has been reached with 1 meaning with 100%.
THE ROLE OF MEANING
What makes a certain difference between classical concepts of an empirical theory and the oksimo paradigm is the role of meaning in the oksimo paradigm. While the classical empirical theory concept is using formal (mathematical) languages for their descriptions with the associated — nearly unsolvable — problem how to relate these concepts to the intended empirical world, does the oksimo paradigm assume the opposite: the starting point is always the ordinary language as basic language which on demand can be extended by special expressions (like e.g. set theoretical expressions, numbers etc.).
Furthermore it is in the oksimo paradigm assumed that the human actors with their built-in meaning function nearly always are able to decided whether an expression e of the used expressions E of the ordinary language L is matching certain properties of the given situation S. Thus the human actors are those who have the authority to decided by their meaning whether some expression is actually true or not.
The same holds with possible goals (visions) and possible inference rules (= change rules). Whether some consequence Y shall happen if some condition X is satisfied by a given actual situation S can only be decided by the human actors. There is no other knowledge available then that what is in the head of the human actors. [1] This knowledge can be narrow, it can even be wrong, but human actors can only decide with that knowledge what is available to them.
If they are using change rules (= inference rules) based on their knowledge and they derive some follow up situation as a theorem, then it can happen, that there exists no empiricial situation S which is matching the theorem. This would be an undefined truth case. If the theorem t would be a contradiction to the given situation S then it would be clear that the theory is inconsistent and therefore something seems to be wrong. Another case cpuld be that the theorem t is matching a situation. This would confirm the belief on the theory.
COMMENTS
[1] Well known knowledge tools are since long libraries and since not so long data-bases. The expressions stored there can only be of use (i) if a human actor knows about these and (ii) knows how to use them. As the amount of stored expressions is increasing the portion of expressions to be cognitively processed by human actors is decreasing. This decrease in the usable portion can be used for a measure of negative complexity which indicates a growng deterioration of the human knowledge space. The idea that certain kinds of algorithms can analyze these growing amounts of expressions instead of the human actor themself is only constructive if the human actor can use the results of these computations within his knowledge space. By general reasons this possibility is very small and with increasing negativ complexity it is declining.
