Journal: uffmm.org,
ISSN 2567-6458, July 20 2019 – May 12, 2020
Email: info@uffmm.org
Author: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de
CONTEXT
This is the next step in the python3 programming project. The overall context is still the python Co-Learning project.
SUBJECT
Meanwhile I am beginning to combine elements of the python language with some applied ideas (in the last section the idea of cognitive entropy illustrated with the equalization of strings). In this section I address the idea of a simple 2-dimensional virtual world, how to represent it with python. In later sections I will use this virtual worlds for some ideas of internal representations and some kinds of learning in an artificial actor.
Remark: for a general help-information you can find a lot of helpful text directly on the python.org site: https://www.python.org/doc/.
SZENARIO
Motivation
Because we want to introduce step-wise artificial actors which can learn, show some intelligence, and can work in teams, we need a minimal virtual world to start (this virtual world is a placeholder for the real world later if applied to the real world (RW) by sensors and actors). Although there is a big difference between the real world and a virtual world a virtual world is nevertheless very helpful for introducing basic concepts. And, indeed, finally if you are applying to real world data you will not be able to do this without mathematical models which represent virtual structures. You will need lots of mappings between real and virtual and vice versa. Thus from a theoretical point of view any kind of virtual model will do, the question is only how ‘easily’ and how ‘good’ it fits.
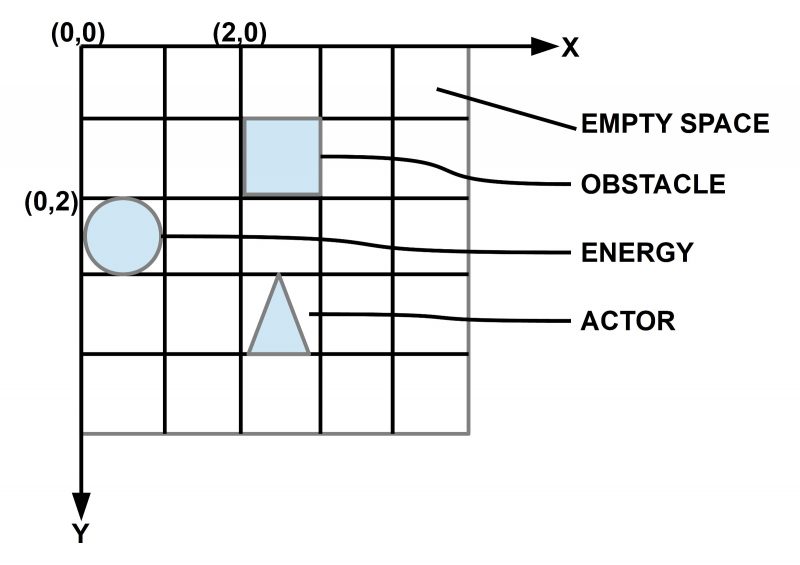
Assumptions Virtual World (VW)
-
A 2-dimensional world as a grid together with a world clock CLCK. The clock produces periodic events which can be used to organize a timely order.
-
There is an x and y axis with the root (0,0) in the upper left corner
-
A coordinate (x,y) represents a position.
-
A position can be occupied by (i) nothing or (ii) by an object. Objects can be obstacles, energy objects (= Food), by a virtual executive actor, or even more.
-
Only one object per position is allowed.
-
It is assumed that there are four directions (headings): ‘North (N)’ as -Y, ‘East (E)’ as +X, ‘South (S)’ as +Y, and ‘West (W)’ as -X.
-
Possible movements are always only in one of the main directions from one cell to the adjacent cell. Movements will be blocked by obstacle objects or actor objects.
-
A sequence of movements realizes in the grid a path from one position to the next.
-
The size of the assumed grids is always finite. In a strict finite world the border of the grid blocks a movement. In a finite-infinite world the borders of the grid are connected in a way that the positions in the south lead to the position in the north and the positions in the east lead to the positions in the west, and vice versa. Therefor can a path in an finite-infinite world become infinite.
-
A grid G with its objects O will be configured at the beginning of an experiment. Without the artificial actors all objects are in a static world assumed to be permanent. In a dynamic world there can be a world function f_w inducing changes depending from the world clock.
-
During an experiment possible changes in the world can happen through a world function f_w, if such a function has been defined. The other possible source for changes are artificial actors, which can act and which can ‘die’.
Remark: The basic idea of this kind of a virtual world I have got from a paper from S.W.Wilson from 1994 entitled ZCS: a zeroth level classifier system published in the Journal Evolutionary Computation vol. 2 number 1 pages 1-18. I have used this concept the first time in a lecture in 2012 (URL: https://www.doeben-henisch.de/fh/gbblt/node95.html). Although this concept looks at a first glance very simple, perhaps too simple, it is very powerful and allows very far reaching experiments (perhaps I can show some aspects from this in upcoming posts :-)).
ACTOR STORY
-
There is a human executive actor as a user who uses a program as an assisting actor by an interface with inputs and outputs.
-
The program tries to construct a 2D-virtual world in the format of a grid. The program needs the size of the grid as (m,n) = (number of columns, number of rows), which is here assumed by default as equal m=n. After the input the program will show the grid on screen.
-
Then the program will ask for the percentage of obstacles ‘O’ and energy objects (= food) ‘F’ in the world. Randomly the grid will be filled according to these values.
-
Then a finite number of virtual actors will be randomly inserted too. In the first version only one.
POSSIBLE EXTENSIONS
In upcoming versions the following options should be added:
-
Allow multiple objects with free selectable strings for encoding.
-
Allow multiple actors.
-
Allow storage of a world specification with reloading in the beginning instead of editing.
-
Transfer the whole world specification into an object specification. This allows the usage of different worlds in one program.
IMPLEMENTATION
And with separation of support functions in an import module:
gridHelper.py(The import module)
EXERCISES
m=int(input(‘Number of columns (= equal to rows!) of 2D-grid ?’))
The input() command generates as output a string object. If one wants to use as output numbers for follow-up computations one has to convert the string object into an integer object, which can be done with the int() operator.
mx=nmlist(n)
Is the call of the nmlist() function which has been defined before the main source code (see. above)(in another version all these supporting functions will again be stored as an extra import module:
printMX(mx,n)
This self-defined function assumes the existence of a matrix object mx with n=m many columns and rows. One row in the matrix can be addressed with the first index of mx like mx[i]. The ‘i’ gives the number of the row from ‘above’ starting with zero. Thus if the matrix has n-many rows then we have [0,…,n-1] as index numbers. The rows correspond to the y-axis.
mx = [[‘_’ for y in range(n)] for x in range(n)]
This expression is an example of a general programming pattern in python called list comprehension (see for example chapters 14 and 22 of the mentioned book of Mark Lutz in part 1 of this series). List comprehension has the basic idea to apply an arbitrary python expression onto an iteration like y in range(n). In the case of a numeric value n=5 the series goes from 0 to 4. Thus y takes the values from 0 to 4. In the above case we have two iterations, one for y (representing the rows) and one vor x (representing the columns). Thus this construct generates (y,x) pairs of numbers which represent virtual positions and each position is associated with a string value ‘_’. And because these instructions are enclosed in []-brackets will the result be a set of lists embedded in a list. And as you can see, it works 🙂 But I must confess that from the general idea of list comprehension to this special application is no direct way. I got this idea from the stack overflow web site (https://stackoverflow.com/questions) which offers lots of discussions around this topic.
for i in range(no):
x=rnd.randrange(n)
y=rnd.randrange(n)
mx[x][y]=obj
A simple for-loop to generate random pairs of (x,y) coordinates to place the different objects into the 2D-grid realized as a matrix object mx.
Demo
PS C:\Users\gdh\code> python vw1.py
Number of columns (= equal to rows!) of 2D-grid ?5
[‘_’, ‘_’, ‘_’, ‘_’, ‘_’]
[‘_’, ‘_’, ‘_’, ‘_’, ‘_’]
[‘_’, ‘_’, ‘_’, ‘_’, ‘_’]
[‘_’, ‘_’, ‘_’, ‘_’, ‘_’]
[‘_’, ‘_’, ‘_’, ‘_’, ‘_’]
Percentage (as integer) of obstacles in the 2D-grid?45
Number of objects :
11
Position :
3 2
Position :
2 3
Position :
3 2
Position :
3 2
Position :
0 1
Position :
2 2
Position :
0 1
Position :
4 3
Position :
0 2
Position :
3 1
Position :
1 4
New Matrix :
[‘_’, ‘O’, ‘O’, ‘_’, ‘_’]
[‘_’, ‘_’, ‘_’, ‘_’, ‘O’]
[‘_’, ‘_’, ‘O’, ‘O’, ‘_’]
[‘_’, ‘O’, ‘O’, ‘_’, ‘_’]
[‘_’, ‘_’, ‘_’, ‘O’, ‘_’]
Percentage (as integer) of Energy Objects (= Food) in the 2D-grid ?15
Number of objects :
3
Position :
3 4
Position :
0 4
Position :
4 1
New Matrix :
[‘_’, ‘O’, ‘O’, ‘_’, ‘F’]
[‘_’, ‘_’, ‘_’, ‘_’, ‘O’]
[‘_’, ‘_’, ‘O’, ‘O’, ‘_’]
[‘_’, ‘O’, ‘O’, ‘_’, ‘F’]
[‘_’, ‘F’, ‘_’, ‘O’, ‘_’]
Default random placement of one virtual actor
Position :
2 2
New Matrix :
[‘_’, ‘O’, ‘O’, ‘_’, ‘F’]
[‘_’, ‘_’, ‘_’, ‘_’, ‘O’]
[‘_’, ‘_’, ‘A’, ‘O’, ‘_’]
[‘_’, ‘O’, ‘O’, ‘_’, ‘F’]
[‘_’, ‘F’, ‘_’, ‘O’, ‘_’]
